
”¾ĢāÄæ”收ŗÆŹżµÄĶ¼ĻóÓėŠŌÖŹ”·ĶŲÕ¹Ń§Ļ°Õ¹Ź¾£ŗ
£ØĪŹĢā£©ČēĶ¼1£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻßG1£ŗ![]() ÓėxÖįĻą½»ÓŚA£Ø-1£¬0£©£¬B£Ø3£¬0£©Į½µć£¬ÓėyÖį½»ÓŚµćC£¬Ōņa= £¬b= £®
ÓėxÖįĻą½»ÓŚA£Ø-1£¬0£©£¬B£Ø3£¬0£©Į½µć£¬ÓėyÖį½»ÓŚµćC£¬Ōņa= £¬b= £®
£Ø²Ł×÷£©½«Ķ¼1ÖŠÅ×ĪļĻßG1ŃŲBC·½ĻņĘ½ŅĘBC³¤¶ČµÄ¾ąĄėµĆµ½Å×ĪļĻßG2£¬G2ŌŚyÖį×ó²ąµÄ²æ·ÖÓėG1ŌŚyÖįÓŅ²ąµÄ²æ·Ö×é³ÉµÄŠĀĶ¼Ļó¼ĒĪŖG£¬ČēĶ¼¢Ś£®ĒėÖ±½ÓŠ“³öĶ¼ĻóG¶ŌÓ¦µÄŗÆŹż½āĪöŹ½£®
£ØĢ½¾æ£©ŌŚĶ¼2ÖŠ£¬¹żµćC×÷Ö±ĻßlĘ½ŠŠÓŚxÖį£¬ÓėĶ¼ĻóG½»ÓŚD£¬EĮ½µć£®ĒóĶ¼ĻóGŌŚÖ±ĻßlÉĻ·½µÄ²æ·Ö¶ŌÓ¦µÄŗÆŹżyĖęxµÄŌö“ó¶ųŌö“óŹ±xµÄȔֵ·¶Ī§£®
£ØÓ¦ÓĆ£©PŹĒÅ×ĪļĻßG2¶Ō³ĘÖįÉĻŅ»øö¶Æµć£¬µ±”÷PDEŹĒÖ±½ĒČż½ĒŠĪŹ±£¬Ö±½ÓŠ“³öPµćµÄ×ų±ź£®

”¾“š°ø”æĪŹĢā£ŗ![]() £¬1£»²Ł×÷£ŗ
£¬1£»²Ł×÷£ŗ £»Ģ½¾æ£ŗ-4£¼x£¼-2»ņ0£¼x£¼1£»Ó¦ÓĆ£ŗ£Ø-2£¬
£»Ģ½¾æ£ŗ-4£¼x£¼-2»ņ0£¼x£¼1£»Ó¦ÓĆ£ŗ£Ø-2£¬![]() +
+![]() £©»ņ£Ø-2£¬
£©»ņ£Ø-2£¬![]() -
-![]() £©.
£©.
”¾½āĪö”æ
ĪŹĢā£ŗĄūÓĆ“ż¶ØĻµŹż·Ø½«AŗĶBµÄ×ų±ź“śČė£¬Ēó³öaŗĶbµÄÖµ¼“æÉ£»
²Ł×÷£ŗøł¾ŻĢāŅāĒó³öĘ½ŅĘŗóµÄÅ×ĪļĻßG2µÄ±ķ“ļŹ½£¬½įŗĻG1µÄ±ķ“ļŹ½¼“æÉµĆ³ö½į¹ū£»
Ģ½¾æ£ŗ»³öĶ¼Ļń£¬Ēó³öĮ½²æ·ÖµÄÅ×ĪļĻߵĶŌ³ĘÖį£¬ŅŌ¼°DŗĶEµÄ×ų±ź£¬½įŗĻæŖæŚ·½Ļņ£¬æɵĆxµÄȔֵ·¶Ī§£»
Ó¦ÓĆ£ŗÓÉĢāŅāÅŠ¶Ļ³ö”ĻDPE=90”ć£¬ŌŚ”÷DPEÖŠĄūÓĆ¹“¹É¶ØĄķĒó³öPQµÄ³¤£¬“Ó¶ųµĆ³öµćP×ų±ź.
½ā£ŗĪŹĢā£ŗ”ßÅ×ĪļĻß![]() ÓėxÖį½»ÓŚA£Ø-1£¬0£©£¬B£Ø3£¬0£©Į½µć£¬
ÓėxÖį½»ÓŚA£Ø-1£¬0£©£¬B£Ø3£¬0£©Į½µć£¬
”ą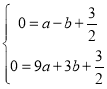 £¬
£¬
½āµĆ£ŗ £¬
£¬
¹Ź“š°øĪŖ£ŗ![]() £¬1£»
£¬1£»
²Ł×÷£ŗ”ßÅ×ĪļĻßG1ŃŲBC·½ĻņĘ½ŅĘBC³¤¶ČµÄ¾ąĄėµĆµ½Å×ĪļĻßG2£¬
B£Ø3,0£©£¬C£Ø0£¬![]() £©£¬
£©£¬![]() £¬
£¬
”ąĘ½ŅĘŗóµÄÅ×ĪļĻßG2µÄ±ķ“ļŹ½ĪŖ![]() £¬
£¬
”ßG2ŌŚyÖį×ó²ąµÄ²æ·ÖÓėG1ŌŚyÖįÓŅ²ąµÄ²æ·Ö×é³ÉµÄŠĀĶ¼Ļó¼ĒĪŖG£¬
”ąĶ¼ĻńGµÄ½āĪöŹ½ĪŖ £»
£»
Ģ½¾æ£ŗÓÉĢāŅāæÉµĆ£ŗµ±x”Ż0Ź±£¬![]() £¬æŖæŚĻņĻĀ£¬¶Ō³ĘÖįĪŖÖ±Ļßx=1£¬
£¬æŖæŚĻņĻĀ£¬¶Ō³ĘÖįĪŖÖ±Ļßx=1£¬
Įīy=0£¬½āµĆ£ŗx1=0£¬x2=2£¬
”ąE£Ø2£¬![]() £©£¬
£©£¬
”ąµ±0£¼x£¼1Ź±£¬yĖęxŌö“ó¶ųŌö“ó£»
µ±x£¼0Ź±£¬![]() £¬æŖæŚĻņĻĀ£¬¶Ō³ĘÖįĪŖÖ±Ļßx=-2£¬
£¬æŖæŚĻņĻĀ£¬¶Ō³ĘÖįĪŖÖ±Ļßx=-2£¬
Įīy=0£¬½āµĆ£ŗx1=-4£¬x2=0£¬
”ąµćD£Ø-4£¬![]() £©£¬
£©£¬
”ąµ±-4£¼x£¼-2Ź±£¬yĖęxŌö“ó¶ųŌö“ó£»
×ŪÉĻ£ŗĶ¼ĻóGŌŚÖ±ĻßlÉĻ·½µÄ²æ·Ö¶ŌÓ¦µÄŗÆŹżyĖęxµÄŌö“ó¶ųŌö“óŹ±£¬
xµÄȔֵ·¶Ī§ŹĒµ±-4£¼x£¼-2»ņ0£¼x£¼1£»
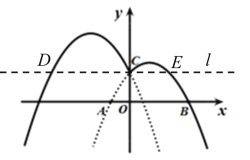
Ó¦ÓĆ£ŗ”ß”÷PDEŹĒÖ±½ĒČż½ĒŠĪ£¬PŹĒÅ×ĪļĻßG2¶Ō³ĘÖįÉĻŅ»øö¶Æµć£¬
”ąÖ»“ęŌŚ”ĻDPE=90”ć£¬
ÓÉĢāŅāµĆ£ŗD£Ø-4£¬![]() £©£¬E£Ø2£¬
£©£¬E£Ø2£¬![]() £©£¬
£©£¬
µ±µćPŌŚÖ±ĻßlÉĻ·½Ź±£¬ČēĶ¼£¬ÉčÖ±ĻßlÓėG2µÄ¶Ō³ĘÖį½»ÓŚµćQ£¬
æɵĆQ£Ø-2£¬![]() £©£¬
£©£¬
”ąDQ=2£¬QE=4£¬DE=6£¬PQ”ĶDE£¬
ÉčPQ=m£¬ŌŚ”÷PDQŗĶ”÷PEQÖŠ£¬
PQ2+DQ2=PD2£¬PQ2+QE2=PE2£¬
¼“![]() £¬
£¬![]() £¬
£¬
ŌŚ”÷PDEÖŠ£¬PD2+PE2=DE2£¬
¼“![]() £¬
£¬
½āµĆ£ŗm=![]() »ņm=
»ņm=![]() £ØÉį£©£¬
£ØÉį£©£¬
”ąm+![]() =
=![]() +
+![]() £¬
£¬
”ąµćPµÄ×ų±źĪŖ£Ø-2£¬![]() +
+![]() £©£¬
£©£¬
µ±µćPŌŚÖ±ĻßlĻĀ·½Ź±£¬Ķ¬ĄķPQ=![]() £¬
£¬
“ĖŹ±µćPµÄ×ų±źĪŖ£Ø-2£¬![]() -
-![]() £©£¬
£©£¬
×ŪÉĻ£ŗµćPµÄ×ų±źĪŖ£Ø-2£¬![]() +
+![]() £©»ņ£Ø-2£¬
£©»ņ£Ø-2£¬![]() -
-![]() £©.
£©.


 ½š°ęæĪĢĆæĪŹ±ŃµĮ·ĻµĮŠ“š°ø
½š°ęæĪĢĆæĪŹ±ŃµĮ·ĻµĮŠ“š°ø µ„ŌŖČ«ÄÜĮ·æ¼¾ķĻµĮŠ“š°ø
µ„ŌŖČ«ÄÜĮ·æ¼¾ķĻµĮŠ“š°ø ŠĀ»ĘøŌ±ų·ØĆܾķĻµĮŠ“š°ø
ŠĀ»ĘøŌ±ų·ØĆܾķĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬½«Å×ĪļĻßy£½©x2+bx+cÓėÖ±Ļßy£½©x+1Ļą½»ÓŚµćA(0£¬1)ŗĶµćB(3£¬©2)£¬½»xÖįÓŚµćC£¬¶„µćĪŖµćF£¬µćDŹĒøĆÅ×ĪļĻßÉĻŅ»µć£®
£Ø1£©ĒóÅ×ĪļĻßµÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©ČēĶ¼1£¬ČōµćDŌŚÖ±ĻßABÉĻ·½µÄÅ×ĪļĻßÉĻ£¬Ēó”÷DABµÄĆ껿×ī“󏱵ćDµÄ×ų±ź£»
£Ø3£©ČēĶ¼2£¬ČōµćDŌŚ¶Ō³ĘÖį×ó²ąµÄÅ×ĪļĻßÉĻ£¬ĒŅµćE£Ø1£¬t£©ŹĒÉäĻßCFÉĻŅ»µć£¬µ±ŅŌC”¢B”¢DĪŖ¶„µćµÄČż½ĒŠĪÓė”÷CAEĻąĖĘŹ±£¬ĒóĖłÓŠĀś×ćĢõ¼žµÄtµÄÖµ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ2019Äź4ŌĀ18ČÕ£¬ĢØĶåŹ”»ØĮ«ÉĘĻß·¢ÉśĄļŹĻ¼¶![]() µŲÕš£¬¾ČŌ®¶Ó¾ČŌ®Ź±£¬ĄūÓĆÉśĆüĢ½²āŅĒŌŚÄ³½ØÖžĪļ·ĻŠęĻĀ·½Ģ½²āµ½µć
µŲÕš£¬¾ČŌ®¶Ó¾ČŌ®Ź±£¬ĄūÓĆÉśĆüĢ½²āŅĒŌŚÄ³½ØÖžĪļ·ĻŠęĻĀ·½Ģ½²āµ½µć![]() “¦ÓŠÉśĆü¼£Ļó£¬ŅŃÖŖ·ĻŠęŅ»²ąµŲĆęÉĻĮ½Ģ½²āµć
“¦ÓŠÉśĆü¼£Ļó£¬ŅŃÖŖ·ĻŠęŅ»²ąµŲĆęÉĻĮ½Ģ½²āµć![]() Ļą¾ą6Ć×£¬Ģ½²āĻßÓėµŲĆęµÄ¼Š½Ē·Ö±šĪŖ
Ļą¾ą6Ć×£¬Ģ½²āĻßÓėµŲĆęµÄ¼Š½Ē·Ö±šĪŖ![]() ŗĶ
ŗĶ![]() £¬ČēĶ¼ĖłŹ¾£¬ŹŌČ·¶ØÉśĆüĖłŌŚµć
£¬ČēĶ¼ĖłŹ¾£¬ŹŌČ·¶ØÉśĆüĖłŌŚµć![]() µÄÉī¶Č(½į¹ū¾«Č·µ½
µÄÉī¶Č(½į¹ū¾«Č·µ½![]() Ć×£¬²Īæ¼Źż¾Ż
Ć×£¬²Īæ¼Źż¾Ż![]() )
)

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
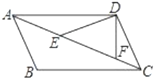
”¾ĢāÄæ”æČēĶ¼£¬![]() ”¢
”¢![]() ŌŚ
ŌŚ![]() µÄ¶Ō½ĒĻß
µÄ¶Ō½ĒĻß![]() ÉĻ£¬
ÉĻ£¬![]() £¬
£¬![]() £¬
£¬![]() £¬Ōņ
£¬Ōņ![]() µÄ“óŠ”ĪŖ£Ø £©£®
µÄ“óŠ”ĪŖ£Ø £©£®
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¶ž“ĪŗÆŹż![]() µÄĶ¼Ļó¾¹żµć
µÄĶ¼Ļó¾¹żµć![]() .
.
£Ø1£©µ±![]() Ź±£¬Čōµć
Ź±£¬Čōµć![]() ŌŚøƶž“ĪŗÆŹżµÄĶ¼ĻóÉĻ£¬Ēóøƶž“ĪŗÆŹżµÄ±ķ“ļŹ½£»
ŌŚøƶž“ĪŗÆŹżµÄĶ¼ĻóÉĻ£¬Ēóøƶž“ĪŗÆŹżµÄ±ķ“ļŹ½£»
£Ø2£©ŅŃÖŖµć![]() £¬
£¬![]() ŌŚøƶž“ĪŗÆŹżµÄĶ¼ĻóÉĻ£¬Ēó
ŌŚøƶž“ĪŗÆŹżµÄĶ¼ĻóÉĻ£¬Ēó![]() µÄȔֵ·¶Ī§£»
µÄȔֵ·¶Ī§£»
£Ø3£©µ±![]() Ź±£¬Čōøƶž“ĪŗÆŹżµÄĶ¼ĻóÓėÖ±Ļß
Ź±£¬Čōøƶž“ĪŗÆŹżµÄĶ¼ĻóÓėÖ±Ļß![]() ½»ÓŚµć
½»ÓŚµć![]() £¬
£¬![]() £¬ĒŅ
£¬ĒŅ![]() £¬Ēó
£¬Ēó![]() µÄÖµ.
µÄÖµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
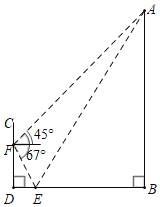
”¾ĢāÄæ”æĪŖĮĖ²āĮæŹśÖ±ĘģøĖABµÄøß¶Č£¬Ä³×ŪŗĻŹµ¼łŠ”×éŌŚµŲĆęD“¦ŹśÖ±·ÅÖƱźøĖCD£¬²¢ŌŚµŲĆęÉĻĖ®Ę½·ÅÖĆŅ»øöĘ½Ćę¾µE£¬Ź¹µĆB£¬E£¬DŌŚĶ¬Ņ»Ė®Ę½ĻßÉĻ£ØČēĶ¼ĖłŹ¾£©£®øĆŠ”×éŌŚ±źøĖµÄF“¦ĶعżĘ½Ćę¾µEĒ”ŗĆ¹Ū²āµ½ĘģøĖ¶„A£Ø“ĖŹ±”ĻAEB£½”ĻFED£©£¬ŌŚF“¦²āµĆĘģøĖ¶„AµÄŃö½ĒĪŖ45”ć£¬Ę½Ćę¾µEµÄø©½ĒĪŖ67”ć£¬²āµĆFD£½2.4Ć×£®ĒóĘģøĖABµÄø߶ČŌ¼ĪŖ¶ąÉŁĆ×£æ£Ø½į¹ū±£ĮōÕūŹż£¬²Īæ¼Źż¾Ż£ŗsin67”ć”Ö![]() £¬cos67”ć”Ö
£¬cos67”ć”Ö![]() £¬tan67”ć”Ö
£¬tan67”ć”Ö![]() £©
£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
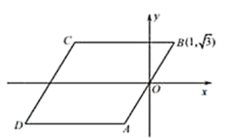
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖĖıߊĪABCDŹĒĮāŠĪ£¬BC”ĪxÖį£¬µćBµÄ×ų±źŹĒ(1£¬![]() )£¬×ų±źŌµćOŹĒABµÄÖŠµć.¶ÆŌ²”ŃPµÄ°ė¾¶ŹĒ
)£¬×ų±źŌµćOŹĒABµÄÖŠµć.¶ÆŌ²”ŃPµÄ°ė¾¶ŹĒ![]() £¬Ō²ŠÄŌŚxÖįÉĻŅĘ¶Æ£¬Čō”ŃPŌŚŌĖ¶Æ¹ż³ĢÖŠÖ»ÓėĮāŠĪABCDµÄŅ»±ßĻąĒŠ£¬ŌņµćPµÄŗį×ų±źm µÄȔֵ·¶Ī§ŹĒ_________£®
£¬Ō²ŠÄŌŚxÖįÉĻŅĘ¶Æ£¬Čō”ŃPŌŚŌĖ¶Æ¹ż³ĢÖŠÖ»ÓėĮāŠĪABCDµÄŅ»±ßĻąĒŠ£¬ŌņµćPµÄŗį×ų±źm µÄȔֵ·¶Ī§ŹĒ_________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
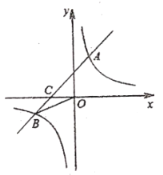
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ņ»“ĪŗÆŹż![]()
![]() µÄĶ¼ĻóÓė·“±ČĄżŗÆŹż
µÄĶ¼ĻóÓė·“±ČĄżŗÆŹż![]()
![]() µÄĶ¼Ļó½»ÓŚŅ»”¢ČżĻóĻŽÄŚµÄ
µÄĶ¼Ļó½»ÓŚŅ»”¢ČżĻóĻŽÄŚµÄ![]() £¬
£¬![]() Į½µć£¬Óė
Į½µć£¬Óė![]() Öį½»ÓŚ
Öį½»ÓŚ![]() µć£¬µć
µć£¬µć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() £¬µć
£¬µć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() £¬
£¬![]() £®
£®
£Ø1£©ĒóøĆ·“±ČĄżŗÆŹżŗĶŅ»“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©Ö±½ÓŠ“³ö¹ŲÓŚ![]() µÄ²»µČŹ½
µÄ²»µČŹ½![]() µÄ½ā¼Æ£»
µÄ½ā¼Æ£»
£Ø3£©Į¬½Ó![]() £¬Ēó
£¬Ēó![]() µÄĆ껿£®
µÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĖıߊĪABCDŹĒĮāŠĪ£¬AB=2£¬ĒŅ”ĻABC=”ĻABE=60”ć£¬MĪŖ¶Ō½ĒĻßBD£Ø²»ŗ¬Bµć£©ÉĻČĪŅāŅ»µć£¬½«BMČʵćBÄꏱÕėŠż×Ŗ60”ćµĆµ½BN£¬Į¬½ÓEN”¢AM”¢CM£¬ŌņAM+BM+CMµÄ×īŠ”ÖµĪŖ_________.

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com