
分析 (1)先同号相加,再异号相加;
(2)先化简,再计算加减法;
(3)(4)根据加法交换律和结合律计算即可求解.
解答 解:(1)-5+3-2
=-7+3
=-4;
(2)-20-(-18)+(-14)+13
=-20+18-14+13
=-34+31
=-3;
(3)5.6+(-0.9)+4.4+(-8.1)
=(5.6+4.4)+(-0.9-8.1)
=10-9
=1;
(4)(+$\frac{3}{2}$)-$\frac{5}{12}$-$\frac{5}{2}$+(-$\frac{7}{12}$)
=(+$\frac{3}{2}$-$\frac{5}{2}$)+(-$\frac{5}{12}$-$\frac{7}{12}$)
=-1-1
=-2.
点评 此题考查了有理数加减混合运算,方法指引:①在一个式子里,有加法也有减法,根据有理数减法法则,把减法都转化成加法,并写成省略括号的和的形式. ②转化成省略括号的代数和的形式,就可以应用加法的运算律,使计算简化.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
 已知二次函数y=-x2+2x+3的图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为D.
已知二次函数y=-x2+2x+3的图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
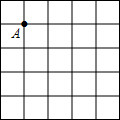 如图,在5×5的正方形网格中,每个小正方形的边长为1,请在所给网格中按下列要求画出图形.
如图,在5×5的正方形网格中,每个小正方形的边长为1,请在所给网格中按下列要求画出图形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
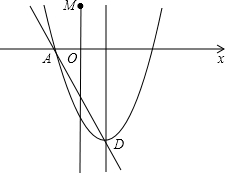 如图所示.抛物线y=x2+bx+c经过A(-1,0),B(4,5)两点.
如图所示.抛物线y=x2+bx+c经过A(-1,0),B(4,5)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com