练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知一次函数y＝kx＋b的图象经过点（0，4）与点（1，2）．
    （1）求一次函数的解析式；
    （2）若一次函数y＝kx＋b的图象还经过点（－1，m）与点（3，n），试比较m，n的大小．

    （1）y＝－2x＋4；（2）m＞n

    解析试题分析：（1）由一次函数y＝kx＋b的图象经过点（0，4）与点（1，2），根据待定系数法求得结果；
    （2）根据一次函数的性质即可判断.
    （1）∵ 一次函数y＝kx＋b的图象经过点（0，4）与点（1，2），
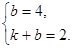    ∴      解得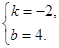
    ∴ 所求一次函数的解析式为y＝－2x＋4；   
    （2）∵ k＝－2＜0，
    ∴ 函数y随自变量x的增大而减小．
    对于一次函数的解析式为y＝－2x＋4图象上的两点（－1，m）与（3，n），
    ∵ －1＜3，
    ∴ m＞n．     
    考点：待定系数法求函数关系式，一次函数的性质
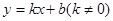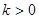    点评：解答本题的关键是熟练掌握一次函数：当时，y随x的增大而增大；当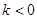时，y随x的增大而减小.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：单选题

    已知一次函数y＝kx-k，若y随x的增大而增大，则它的图像经过


    1. A.
      第一、二、三象限
    2. B.
      第一、三、四象限
    3. C.
      第一、二、四象限
    4. D.
      第二、三、四象限

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知一次函数y1＝kx＋b与反比例函数y2＝在同一直角坐标系中的图象如图所示，则当y1＜y2时，x的取值范围是【   】
    A．x＜－1或0＜x＜3B．－1＜x＜0或x＞3
    C．－1＜x＜0D．x＞3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    (8分)已知一次函数y＝kx－4，当x＝2时，y＝－3．
    (1)求一次函数的解析式；
    (2)将该函数的图象向上平移6个单位，求平移后的图象与x轴交点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知一次函数y＝kx＋b的图象经过点（－1，－4），且与正比例函数y＝x+1的图象相交于点（2，a），求

    （1）a的值

    （2）k，b的值

    （3）这两个函数图象与x轴所围成的三角形面积.

    查看答案和解析>>

    科目：初中数学 来源：2012届山东省济宁地区九年级第一学期期中考试数学试卷 题型：解答题

    在平面直角坐标系xOy中，二次函数y＝mx2＋(m－3)x－3（m＞0）的图象与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C．

    1.求点A的坐标；

    2.当∠ABC＝45°时，求m的值；

    3.已知一次函数y＝kx＋b，点P(n，0)是x轴上的一个动点，在（2）的条件下，过点P垂直于x轴的直线交这个一次函数的图象于点M，交二次函数y＝mx2＋(m－3)x－3（m＞0）的图象于点N．若只有当－2＜n＜2时，点M位于点N的上方，求这个一次函数的解析式．（友情提示：自画图形）

     

    查看答案和解析>>

    同步练习册答案