
����Ŀ��������ABCD�У���ABC��60����P������BD��һ���㣬��APΪ�����Ҳ����ȱ���APE������CE��
��1����ͼ1������P������ABCD�ڲ�ʱ����BP��CE��������ϵ���� ����CE��AD��λ�ù�ϵ���� ����
��2����ͼ2������P������ABCD�ⲿʱ����1���еĽ����Ƿ�������������������֤����������������˵�����ɣ�
��3����ͼ2������BE����AB��2![]() ��BE��2
��BE��2![]() ����AP�ij���
����AP�ij���

���𰸡���1��BP=CE��CE��AD����2��������Ȼ���������ɼ���������3��2![]()
��������
��1��������ABCD�͡�ABC=60����֤��ABC����ACD�ǵȱ������Σ��ɵȱ���APE�ɵ�AP=AE����PAE=��BAC=60������ȥ�����ǡ�PAC�á�BAP=��CAE������SAS��֤����BAP�ա�CAE������BP=CE����ABP=��ACE�������ζԽ���ƽ��һ��Խǿ�֤��ABP=30�����ʡ�ACE=30����CEƽ�֡�ACD����AC=CD�������������ߺ�һ�ɵ�CE��AD��
��2�����۲��䣮֤������ͬ��1����
��3����Rt��AOP�У����OA��OP���ɽ�����⣮
��1��BP=CE��CE��AD��
���ɣ�������ABCD�У���ABC=60��
��AB=BC=CD=AD����ADC=��ABC=60��
���ABC����ACD�ǵȱ�������
��AB=AC��AC=CD����BAC=��ACD=60��
�ߡ�APE�ǵȱ�������
��AP=AE����PAE=60��
���BAC-��PAC=��PAE-��PAC
����BAP=��CAE��
���BAP�ա�CAE��SAS��
��BP=CE����ABP=��ACE
��BDƽ�֡�ABC
���ACE=��ABP=![]() ��ABC=30��
��ABC=30��
��CEƽ�֡�ACD
��CE��AD��
�ʴ�ΪBP=CE��CE��AD��
��2��������Ȼ�������������£���ͼ����CE��AD��H������AC��
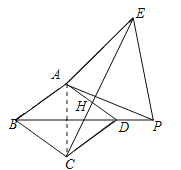
���ı���ABCD�����Σ���ABC=60����
���ABC����ACD���ǵȱ������Σ���ABD=��CBD=30����
�ߡ�APE�ǵȱ������Σ�
��AB=AC��AP=AE����BAC=��PAE=60����
���BAP�ա�CAE��
��BP=CE����ABP=��ACE=30����
�ߡ�CAH=60����
���CAH+��ACH=90����
���AHC=90������CE��AD��
��3����ͼ������BE��
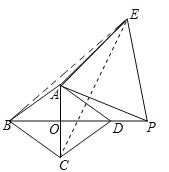
�ɣ�2����֪CE��AD��BP= CE��
������ABCD��AD��BC����CE��BC��
��BC=AB=2![]() ��BE=2
��BE=2![]() ��
��
��Rt��BCE��CE=![]() =8��
=8��
��BP=CE=8��
��AC��BD�����εĶԽ��ߣ�
���ABD=![]() ��ABC=30����AC��BD��
��ABC=30����AC��BD��
��OA=![]() AB=
AB=![]() ��BO=
��BO=![]() =3��
=3��
��OP=BP��BO=5��
��Rt��AOP��AP=![]() =2
=2![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ι��ţ���������ˮ��2mʱ��ˮ���4m����ˮ���½�1mʱ��ˮ���������_____m��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x��һԪ���η���x2+��2k+1��x+k2+1=0����������ʵ��x1��x2��
��1����ʵ��k��ȡֵ��Χ��
��2����������ʵ��x1��x2����x1+x2=��x1x2����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣��ڡ�ABC�У�AB=AC����AB��һ��D��DE��AC��BC�ڵ�E����EΪ���㣬EDΪһ�ߣ�����DEF=��A����һ��EF��AC�ڵ�F��
��1����֤���ı���ADEFΪƽ���ı��Σ�
��2������DΪAB�е�ʱ���ж�ADEF����״��
��3���ӳ�ͼ���е�DE����G��ʹEG=DE������AE��AG��FG���õ�ͼ�ڣ���AD=AG���ж��ı���AEGF����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10�֣���ͼ����֪Rt��ABC�У���C=90�㣬DΪBC���е㣬��ACΪֱ���ġ�O��AB�ڵ�E��
��1����֤��DE�ǡ�O�����ߣ�
��2����AE��EB=1��2��BC=6�����O�İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�BEƽ����ABC��AD�ڵ�E��DFƽ����ADC��BC�ڵ�F��
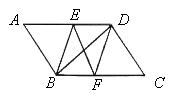
��1����ABE�ա�CDF
��2����BD��EF�����ж��ı���EBFD��ʲô�����ı��Σ���֤����Ľ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ABCD�У��Խ���AC��BD�ཻ�ڵ�E������ABC��AC����ֱ�߷�������AB��C������B������ΪB��������B��D��B��C������B��C��AD�ཻ�ڵ�G��
����AGC�ǵ��������Σ�����B��ED�ǵ��������Σ�
����B��GD�ǵ��������Σ���AC��B��D��
������AEB��45����BD��2����DB���ij�Ϊ![]() ��
��
������ȷ���У�����������

A. 2B. 3C. 4D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһֱ������ϵ�У���һ�κ���y��x��3��x��1����ͼ����ֱ��x��2��������Ϊ2�����е㹹�ɸ�ֱ�ߣ�����ಿ����ֱ��x��2���ۣ�ͼ������ಿ�ֱ��ֲ��䣬�õ�һ����ͼ��������x�ĺ���y��2x+b��ͼ�����ͼ�������������㣬��b��ȡֵ��Χ�ǣ�������

A. 8��b��5B. ��8��b����5C. ��8��b����5D. ��8��b����5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����������ӵ�һ����һ��ׯC���ӱ�ԭ������ȡˮ��A��B������AB��AC������ij��ԭ����C��A��·�����Ѿ���ͨ��ij��Ϊ�������ȡˮ�����ںӱ��½�һ��ȡˮ��H��A��H��B��һ��ֱ���ϣ���������һ��·CH�����CB��3ǧ�ף�CH��2.4ǧ�ף�HB��1.8ǧ�ף�
��1����CH�Ƿ�Ϊ�Ӵ�ׯC���ӱߵ����·�������ʣ�CH��AB�Ƿ�ֱ������ͨ���������˵����
��2����ԭ����·��AC�ij���

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com