
【题目】如图,在△ABC中,AD是BC上的中线,点E在线段AC上且EC=2AE,线段AD与线段BE交于点F,若△ABC对面积为3,则四边形EFDC的面积为__________.

【答案】![]()
【解析】
连接CF,根据CE=2AE,△ABC的面积为3可知S△ABE=![]() ×3=1,S△CEF=
×3=1,S△CEF=![]() ×3=2,S△AEF:S△CEF=1:2,设S△AEF=S,则S△CEF=2S故S△ABF=1-S,则S△BCF=2-2S,设S△ABF=x=1-S,则S△BCF=2x=2-2S,由AD是BC边上的中线可知S△BDF=S△CDF=x,2x=x+3S,即x=3S,所以S△ABC=12S,S四边形EFDC=5S,由此可得出结论.
×3=2,S△AEF:S△CEF=1:2,设S△AEF=S,则S△CEF=2S故S△ABF=1-S,则S△BCF=2-2S,设S△ABF=x=1-S,则S△BCF=2x=2-2S,由AD是BC边上的中线可知S△BDF=S△CDF=x,2x=x+3S,即x=3S,所以S△ABC=12S,S四边形EFDC=5S,由此可得出结论.
连接CF,
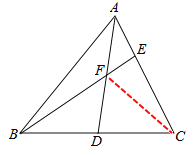
∵CE=2AE,△ABC的面积为3,
∴S△ABE=![]() ×3=1,S△BCE=
×3=1,S△BCE=![]() ×3=2,
×3=2,
S△AEF:S△CEF=1:2,
设S△AEF=S,则S△CEF=2S,
∴S△AFB=1-S,则S△BCF=2-2S,
设S△ABF=x=1-S,则S△BCF=2x=2-2S,
∵AD是BC边上的中线,
∴S△BDF=S△CDF=x,2x=x+3S,即x=3S,
∴S△ABC=12S,S四边形EFDC=5S,
∴![]() .
.
∴S四边形EFDC=![]() =
= ![]() .
.
故答案为:![]() .
.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,求
,求![]() 的度数.
的度数.

(1)填空,在空白处填上结果或者理由.
解:过点![]() 作
作![]() ,(如图)
,(如图)
得![]() ___________°, ( )
___________°, ( )
又因为![]() ,(已知)
,(已知)
所以![]() ___________°.
___________°.
因为![]() ,
,
所以![]() , ( )
, ( )
又因为![]() ,(已知)
,(已知)
所以![]() ___________°,
___________°,
所以![]() ___________°.
___________°.
(2)请用另一种解法求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
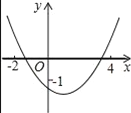
A. c>﹣1 B. b>0 C. 2a+b≠0 D. 9a+c>3b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某厂制作甲、乙两种环保包装盒。已知同样用6m的材料制成甲盒的个数比制成乙盒的个数少2个,且制成一个甲盒比制作一个乙盒需要多用20%的材料。
(1)求制作每个甲盒、乙盒各用多少材料?
(2)如果制作甲、乙两种包装盒3000个,且甲盒的数量不少于乙盒数量的2倍,那么请写出所需材料总长度![]() 与甲盒数量
与甲盒数量![]() 之间的函数关系式,并求出最少需要多少米材料。
之间的函数关系式,并求出最少需要多少米材料。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN∥OP,点A为直线MN上一定点,B为直线OP上的动点,在直线MN与OP之间且在线段AB的右方作点D,使得AD⊥BD.设∠DAB=α(α为锐角).
(1)求∠NAD与∠PBD的和;(提示过点D作EF∥MN)
(2)当点B在直线OP上运动时,试说明∠OBD﹣∠NAD=90°;
(3)当点B在直线OP上运动的过程中,若AD平分∠NAB,AB也恰好平分∠OBD,请求出此时α的值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,作斜边AB上中线CD,得到第1个三角形ACD;
,作斜边AB上中线CD,得到第1个三角形ACD;![]() 于点E,作
于点E,作![]() 斜边DB上中线EF,得到第2个三角形DEF;依次作下去
斜边DB上中线EF,得到第2个三角形DEF;依次作下去![]() 则第1个三角形的面积等于______,第n个三角形的面积等于______.
则第1个三角形的面积等于______,第n个三角形的面积等于______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 中
中![]() ,
,![]() ,
,![]() .
.
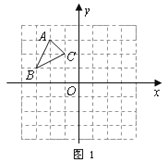
(1)将![]() 向右平移
向右平移![]() 个单位长度,画出平移后的
个单位长度,画出平移后的![]() ;
;
(2)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(3)将![]() 绕原点
绕原点![]() 旋转
旋转![]() ,画出旋转后的
,画出旋转后的![]() ;
;
(4)在![]() ,
,![]() ,
,![]() 中,
中,
![]() ______与
______与![]() ______成轴对称,对称轴是______;
______成轴对称,对称轴是______;
![]() ______与
______与![]() ______成中心对称,对称中心的坐标是____.
______成中心对称,对称中心的坐标是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( )
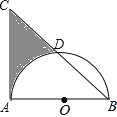
A. 16 B. 24-4π C. 32-4π D. 32-8π
查看答案和解析>>
科目:初中数学 来源: 题型:
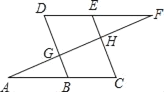
【题目】如图,E在直线DF上,B在直线AC上,若∠AGB=∠EHF,∠C=∠D,试判断∠A与∠F的关系,并说明理由.
说明:
因为∠AGB=∠EHF(已知)
∠AGB= (依据: )
所以 ,(等量代换)
所以 (依据: )
所以∠C= ,(依据: )
又因为∠C=∠D,(已知)
所以 ,(等量代换)
所以DF∥AC(依据: )
所以∠A=∠F.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com