
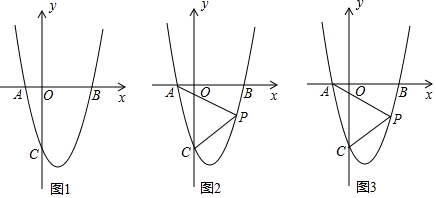
Ζ÷Έω Θ®1Θ©ΫβΖΫ≥ΧΒΟΒΫx1=-mΘ§x2=3Θ§«σΒΟBΘ®3Θ§0Θ©Θ§AΘ®-mΘ§0Θ©Θ§ΗυΨί“―÷ΣΧθΦΰΒΟΒΫΫα¬έΘΜ
Θ®2Θ©ΙΐPΉςPFΓΆx÷α”ΎFΘ§…ηFΘ®tΘ§0Θ©Θ§ΒΟΒΫAF=t+1Θ§PF=-aΘ®t+1Θ©Θ®t-3Θ©Θ§«σΒΟtanΓœFAP=$\frac{PF}{PA}$-aΘ®t-3Θ©Θ§ΒΟΒΫ$\frac{OD}{OA}$=-aΘ®t-3Θ©«σΒΟa=1Θ§”Ύ «ΒΟΒΫΫα¬έΘΜ
Θ®3Θ©ΗυΨί»ΐΫ«–ΈΒΡΟφΜΐΝ–ΖΫ≥ΧΒΟΒΫt=$\frac{5}{2}$Θ§«σΒΟPΘ®$\frac{5}{2}$Θ§-$\frac{7}{4}$Θ©Θ§ΒΟΒΫAM=$\frac{7}{2}$Θ§PM=$\frac{7}{4}$Θ§tanΓœMAP=$\frac{1}{2}$Θ§”Ύ «ΒΟΒΫMN=$\frac{21}{4}$Θ§ΙΐMΉςMKΓΆAP”ΎKΘ§ΙΐFΉςFRΓΆx÷α”ΎRΘ§ΒΟΒΫΓςMKF «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§…ηAF=FK=MK=xΘ§ΗυΨίΙ¥Ι…Ε®άμΒΟΒΫFM=$\sqrt{2}$xΘ§«σΒΟFR=$\frac{\sqrt{5}}{5}$xΘ§Ϋβ÷±Ϋ«»ΐΫ«–ΈΦ¥Ω…ΒΟΒΫΫα¬έΘ°
Ϋβ¥π 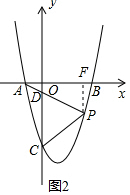 ΫβΘΚΘ®1Θ©ΓΏaΓΌ0Θ§
ΫβΘΚΘ®1Θ©ΓΏaΓΌ0Θ§
ΓύΘ®x+mΘ©Θ®x-3Θ©=0Θ§
Γύx1=-mΘ§x2=3Θ§
ΓύBΘ®3Θ§0Θ©Θ§AΘ®-mΘ§0Θ©Θ§
ΓΏAB=4Θ§
Γύ3+m=4Θ§
Γύm=1Θ§
ΓύAΘ®-1Θ§0Θ©ΘΜ
Θ®2Θ©ΙΐPΉςPFΓΆx÷α”ΎFΘ§
…ηFΘ®tΘ§0Θ©Θ§
ΓύAF=t+1Θ§PF=-aΘ®t+1Θ©Θ®t-3Θ©Θ§
ΓύtanΓœFAP=$\frac{PF}{PA}$-aΘ®t-3Θ©Θ§
Γύ$\frac{OD}{OA}$=-aΘ®t-3Θ©Θ§
ΓύOD=aΘ®t-3Θ©Θ§
ΓύD[0Θ§aΘ®t-3Θ©]Θ§
“ΉΒΟCΘ®0Θ§-3aΘ©Θ§
ΓύCD=tΘ§
ΓύaΘ®t-3Θ©+3a=tΘ§
Γύat=tΘ§Γύa=1Θ§
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=x2-2x-3ΘΜ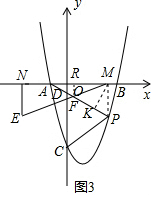 Θ®3Θ©ΓΏSΓςCDP=$\frac{25}{8}$Θ§
Θ®3Θ©ΓΏSΓςCDP=$\frac{25}{8}$Θ§
Γύ$\frac{1}{2}$Θ®3+t-3Θ©ΓΝt=$\frac{25}{8}$Θ§
Γύt=$\frac{5}{2}$Θ§
ΓύPΘ®$\frac{5}{2}$Θ§-$\frac{7}{4}$Θ©Θ§
ΓύAM=$\frac{7}{2}$Θ§PM=$\frac{7}{4}$Θ§
ΓύtanΓœMAP=$\frac{1}{2}$Θ§
ÿAN=PMȧ
ΓύAN=$\frac{7}{4}$Θ§
ΓύMN=$\frac{21}{4}$Θ§
ΙΐMΉςMKΓΆAP”ΎKΘ§
ΓύΓςMKF «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓύMK=FKΘ§
ΓύAF=FK=MKΘ§
…ηAF=FK=MK=xΘ§
ΓύFM=$\sqrt{2}$xΘ§
ΓΏtanΓœMAP=$\frac{1}{2}$Θ§
ΓύFR=$\frac{\sqrt{5}}{5}$xΘ§
ΓύRM=$\sqrt{M{F}^{2}-R{F}^{2}}$=$\frac{3\sqrt{5}}{5}$xΘ§
ΓύtanΓœRMF=$\frac{FR}{RM}$=$\frac{1}{3}$Θ§
Γύ$\frac{MN}{NE}$=$\frac{1}{3}$Θ§
ΓύNE=$\frac{7}{4}$Θ§
ΓύEΘ®-$\frac{11}{4}$Θ§-$\frac{7}{4}$Θ©Θ°
ΒψΤά ±ΨΧβΩΦ≤ιΝΥ¥ΐΕ®œΒ ΐΖ®«σΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΘ§»ΐΫ«–ΈΒΡΟφΜΐΘ§Ι¥Ι…Ε®άμΘ§Ϋβ÷±Ϋ«»ΐΫ«–ΈΘ§’ΐ»ΖΒΡΉς≥ωΗ®÷ζœΏ «ΫβΧβΒΡΙΊΦϋΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 30ΓψΘ§60ΓψΘ§90Γψ | BΘ° | 60ΓψΘ§120ΓψΘ§180Γψ | CΘ° | 50ΓψΘ§100ΓψΘ§150Γψ | DΘ° | 80ΓψΘ§120ΓψΘ§160Γψ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 5 | BΘ° | 4 | CΘ° | 3 | DΘ° | 2.4 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
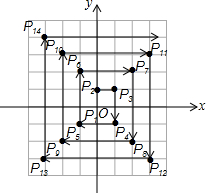 »γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΟΩΗωΉν–ΓΖΫΗώΒΡ±Ώ≥ΛΨυΈΣ1ΗωΒΞΈΜ≥ΛΕ»Θ§P1Θ§P2Θ§P3Θ§Γ≠Ψυ‘ΎΗώΒψ…œΘ§ΤδΥ≥–ρΑ¥ΆΦ÷–ΓΑΓζΓ±ΖΫœρ≈≈Ν–Θ§»γΘΚP1Θ®0Θ§0Θ©Θ§P2Θ®0Θ§1Θ©Θ§P3Θ®1Θ§1Θ©Θ§P4Θ®1Θ§-1Θ©Θ§P5Θ®-1Θ§-1Θ©Θ§P6Θ®-1Θ§2Θ©Γ≠ΗυΨί’βΗωΙφ¬…Θ§ΒψP2017ΒΡΉχ±ξΈΣΘ®ΓΓΓΓΘ©
»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΟΩΗωΉν–ΓΖΫΗώΒΡ±Ώ≥ΛΨυΈΣ1ΗωΒΞΈΜ≥ΛΕ»Θ§P1Θ§P2Θ§P3Θ§Γ≠Ψυ‘ΎΗώΒψ…œΘ§ΤδΥ≥–ρΑ¥ΆΦ÷–ΓΑΓζΓ±ΖΫœρ≈≈Ν–Θ§»γΘΚP1Θ®0Θ§0Θ©Θ§P2Θ®0Θ§1Θ©Θ§P3Θ®1Θ§1Θ©Θ§P4Θ®1Θ§-1Θ©Θ§P5Θ®-1Θ§-1Θ©Θ§P6Θ®-1Θ§2Θ©Γ≠ΗυΨί’βΗωΙφ¬…Θ§ΒψP2017ΒΡΉχ±ξΈΣΘ®ΓΓΓΓΘ©| AΘ° | Θ®-504Θ§-504Θ© | BΘ° | Θ®-505Θ§-504Θ© | CΘ° | Θ®504Θ§-504Θ© | DΘ° | Θ®-504Θ§505Θ© |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
 »γΆΦΘ§“―÷ΣΘ§ΒψAΘ®0Θ§0Θ©ΓΔBΘ®4$\sqrt{3}$Θ§0Θ©ΓΔCΘ®0Θ§4Θ©Θ§‘ΎΓςABCΡΎ“ά¥ΈΉςΒ»±Ώ»ΐΫ«–ΈΘ§ Ι“Μ±Ώ‘Ύx÷α…œΘ§Νμ“ΜΗωΕΞΒψ‘ΎBC±Ώ…œΘ§Ής≥ωΒΡΒ»±Ώ»ΐΫ«–ΈΖ÷±π «ΒΎ1ΗωΓςAA1B1Θ§ΒΎ2ΗωΓςB1A2B2Θ§ΒΎ3ΗωΓςB2A3B3Θ§Γ≠‘ρΒΎ2017ΗωΒ»±Ώ»ΐΫ«–ΈΒΡ±Ώ≥ΛΒ»”ΎΘ®ΓΓΓΓΘ©
»γΆΦΘ§“―÷ΣΘ§ΒψAΘ®0Θ§0Θ©ΓΔBΘ®4$\sqrt{3}$Θ§0Θ©ΓΔCΘ®0Θ§4Θ©Θ§‘ΎΓςABCΡΎ“ά¥ΈΉςΒ»±Ώ»ΐΫ«–ΈΘ§ Ι“Μ±Ώ‘Ύx÷α…œΘ§Νμ“ΜΗωΕΞΒψ‘ΎBC±Ώ…œΘ§Ής≥ωΒΡΒ»±Ώ»ΐΫ«–ΈΖ÷±π «ΒΎ1ΗωΓςAA1B1Θ§ΒΎ2ΗωΓςB1A2B2Θ§ΒΎ3ΗωΓςB2A3B3Θ§Γ≠‘ρΒΎ2017ΗωΒ»±Ώ»ΐΫ«–ΈΒΡ±Ώ≥ΛΒ»”ΎΘ®ΓΓΓΓΘ©| AΘ° | $\frac{\sqrt{3}}{{2}^{2015}}$ | BΘ° | $\frac{\sqrt{3}}{{2}^{2016}}$ | CΘ° | $\frac{\sqrt{3}}{{2}^{2017}}$ | DΘ° | $\frac{\sqrt{3}}{{2}^{2019}}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 8ΒΡΝΔΖΫΗυ «Γά2 | |
| BΘ° | $\sqrt{8}$ «“ΜΗωΉνΦρΕΰ¥ΈΗυ Ϋ | |
| CΘ° | Κ· ΐy=$\frac{1}{x-1}$ΒΡΉ‘±δΝΩxΒΡ»Γ÷ΒΖΕΈß «xΘΨ1 | |
| DΘ° | ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΒψPΘ®2Θ§3Θ©”κΒψQΘ®-2Θ§3Θ©ΙΊ”Ύy÷αΕ‘≥Τ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com