
【题目】如图,在四边形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC 
(1)求证:△ABD≌△ECB;
(2)若∠EDC=65°,求∠ECB的度数;
(3)若AD=3,AB=4,求DC的长.
【答案】
(1)证明:∵AD∥BC,
∴∠ADB=∠EBC,
∵∠A=∠CEB=90°,
在△ABD与△CEB中, 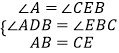 ,
,
∴△ABD≌△ECB
(2)解:由(1)证得△ABD≌△ECB,
∴BD=BC,
∴∠BCD=∠BDC=65°,
∵∠DCE=90°﹣65°=25°,
∴∠ECB=40°
(3)解:由(1)证得△ABD≌△ECB,
∴CE=AB=4,BE=AB=3,
∴BD=BC= ![]() =5,
=5,
∴DE=2,
∴CD= ![]() =2
=2 ![]()
【解析】(1)由AD∥BC,得到∠ADB=∠EBC,又因为∠A=∠CEB=90°,推出△ABD≌△ECB;(2)根据等腰三角形的性质和直角三角形的性质得到结果;(3)由全等三角形的性质得到对应边相等,利用勾股定理解出结果.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线EF与AB交于点M,与CD交于点O,OG平分∠DOF,若∠COM=120°,∠EMB=![]() ∠COF.
∠COF.

(1)求∠FOG的度数;
(2)写出一个与∠FOG互为同位角的角;
(3)求∠AMO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】花粉的质量很小,一粒某种植物花粉的质量约为0.000037毫克,已知1克=1000毫克,那么0.000037毫克可用科学记数法表示为
A. 3.7×10﹣5克 B. 3.7×10﹣6克 C. 37×10﹣7克 D. 3.7×10﹣8克
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x、y轴上,连接AC,将纸片OABC沿AC折叠,使点B落在点D的位置.若点B的坐标为(2,4),则点D的横坐标是___________.
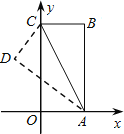
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,在直角梯形ABCD中,∠BAD=90°,E是直线AB上一点,过E作直线l∥BC,交直线CD于点F.将直线l向右平移,设平移距离BE为t(t≥0),直角梯形ABCD被直线l扫过的面积(图中阴影部分)为S,S关于t的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
信息读取
(1)梯形上底的长AB=;
(2)直角梯形ABCD的面积=;
图象理解
(3)写出图②中射线NQ表示的实际意义;
(4)当2<t<4时,求S关于t的函数关系式;
问题解决
(5)当t为何值时,直线l将直角梯形ABCD分成的两部分面积之比为1:3.
查看答案和解析>>
科目:初中数学 来源: 题型:
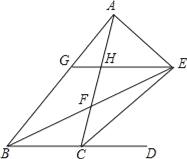
【题目】如图,△ABC的内角∠ABC和外角∠ACD的平分线相交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论:
①∠BEC=![]() ∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正确的结论有_____(将所有正确答案的序号填写在横线上).
∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正确的结论有_____(将所有正确答案的序号填写在横线上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为8cm2 , AP垂直∠B的平分线BP于P,则△PBC的面积为( )
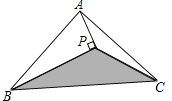
A. 2cm2 B. 3cm2 C. 4cm2 D. 5cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com