
【题目】阅读下面材料:
已知:如图,在正方形ABCD中,边![]() .
.
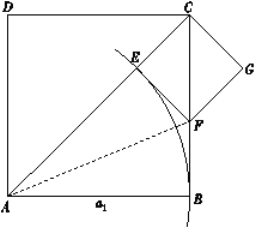
按照以下操作步骤,可以从该正方形开始,构造一系列的正方形,它们之间的边满足一定的关系,并且一个比一个小.
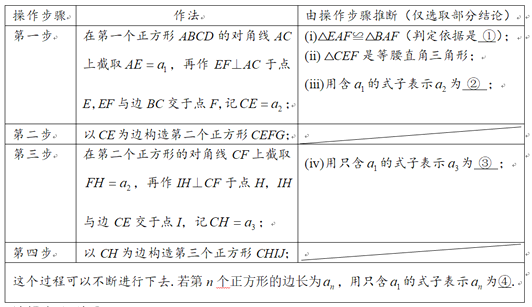
请解决以下问题:
(1)完成表格中的填空:
① ;② ;
③ ;④ ;
(2)根据以上第三步、第四步的作法画出第三个正方形CHIJ(不要求尺规作图).
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,延长BA到点F,使得AF=AB,连接FC交AD于E.

(1)求证:AD与FC互相平分;
(2)当CF平分∠BCD时,BC与CD的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文化,源远流长.在文学方面,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查.根据调查结果绘制成如所示的两个不完整的统计图,请结合图中信息解决下列问题:
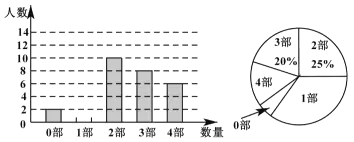
(1) 本次调查一共抽取了______名学生;扇形统计图中“1部”所在扇形的圆心角为______度
(2) 若该中学有1000名学生,请估计至少阅读3部四大古典名著的学生有多少名?
(3) 没有读过四大名著的两名学生准备从四大古典名著中各自随机选择一部来阅读,则他们选中同一名著的概率为_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料一:
早在2011年9月25日,北京故宫博物院就开始尝试网络预售门票,2011年全年网络售票仅占1.68%.2012年至2014年,全年网络售票占比都在2%左右.2015年全年网络售票占17.33%,2016年全年网络售票占比增长至41.14%.2017年8月实现网络售票占比77%.2017年10月2日,首次实现全部网上售票.与此同时,网络购票也采用了“人性化”的服务方式,为没有线上支付能力的观众提供代客下单服务.实现全网络售票措施后,在北京故宫博物院的精细化管理下,观众可以更自主地安排自己的行程计划,获得更美好的文化空间和参观体验.
材料二:
以下是某同学根据网上搜集的数据制作的2013-2017年度中国国家博物馆参观人数及年增长率统计表.
年度 | 2013 | 2014 | 2015 | 2016 | 2017 |
参观人数(人次) | 7 450 000 | 7 630 000 | 7 290 000 | 7 550 000 | 8 060 000 |
年增长率(%) | 38.7 | 2.4 | -4.5 | 3.6 | 6.8 |

他还注意到了如下的一则新闻:2018年3月8日,中国国家博物馆官方微博发文,宣布取消纸质门票,观众持身份证预约即可参观. 国博正在建设智慧国家博物馆,同时馆方工作人员担心的是:“虽然有故宫免(纸质)票的经验在前,但对于国博来说这项工作仍有新的挑战.参观故宫需要观众网上付费购买门票,他遵守预约的程度是不一样的.但(国博)免费就有可能约了不来,挤占资源,所以难度其实不一样.” 尽管如此,国博仍将积极采取技术和服务升级,希望带给观众一个更完美的体验方式.
根据以上信息解决下列问题:
(1)补全以下两个统计图;
(2)请你预估2018年中国国家博物馆的参观人数,并说明你的预估理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴的正半轴、y轴的正半轴上,且OA、OC(![]() )的长是方程
)的长是方程![]() 的两个根.
的两个根.
(1)如图,求点A的坐标;
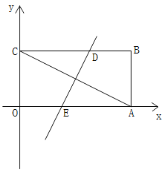
(2)如图,将矩形OABC沿某条直线折叠,使点A与点C重合,折痕交CB于点D,交OA于点E.求直线DE的解析式;

(3)在(2)的条件下,点P在直线DE上,在直线AC上是否存在点Q,使以点A、B、P、Q为顶点的四边形是平行四边形.若存在,请求出点Q坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳池普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元张,每次凭卡不再收费;
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常销售,两种优惠卡仅限暑假使用,每人一次一张票不限次数.
(1)分别写出选择普通票、银卡消费时,所需费用![]() 、
、![]() 与次数
与次数![]() 之间的函数表达式;
之间的函数表达式;
(2)小明打算暑假每天游泳一次,按55天计算,则选择哪种消费方式更合算?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P、Q在数轴上表示的数分别是-8、4,点P以每秒2个单位的速度运动,点Q以每秒1个单位的速度运动.设点P、Q同时出发向右运动,运动时间为t秒.

(1)若运动2秒时,则点P表示的数为_______,点P、Q之间的距离是______个单位;
(2)求经过多少秒后,点P、Q重合?
(3)试探究:经过多少秒后,点P、Q两点间的距离为6个单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a﹣b=0;②abc<0;③抛物线与x轴的另一个交点坐标是(3,0);④方程ax2+bx+c﹣3=0有两个相等的实数根;⑤当﹣4<x<﹣1时,则y2<y1.
其中正确的是( )

A. ①②③ B. ①③⑤ C. ①④⑤ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意四个有理数![]() ,可以组成两个有理数对
,可以组成两个有理数对![]() 与
与![]() .
.
我们规定:![]() .
.
例如:![]() .
.
根据上述规定解决下列问题:
(1)有理数对![]() ;
;
(2)若有理数对![]() ,则
,则![]() ;
;
(3)当满足等式![]() 的
的![]() 是整数时,求整数
是整数时,求整数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com