
【题目】如图,△ABC、△DEP是两个全等的等腰直角三角形,∠BAC=∠PDE=90°.
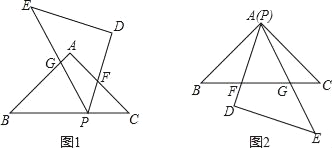
(1)若将△DEP的顶点P放在BC上(如图1),PD、PE分别与AC、AB相交于点F、G.求证:△PBG∽△FCP;
(2)若使△DEP的顶点P与顶点A重合(如图2),PD、PE与BC相交于点F、G.试问△PBG与△FCP还相似吗?为什么?
【答案】(1)证明见解析(2)△PBG与△FCP相似
【解析】试题分析:(1)已知△ABC、△DEP是两个全等的等腰直角三角形,即可得∠B=∠C=∠DPE=45°,∠BPG+∠CPF=135°;在△BPG中,∠B=45°,∠BPG+∠BGP=135°,由此可得∠BGP=∠CPF,再由∠B=∠C,根据两角对应相等的两个三角形相似即可得△PBG∽△FCP;(2)△PBG与△FCP相似,由△ABC、△DEP是两个全等的等腰直角三角形,可得∠B=∠C=∠DPE=45°,又因∠BGP=∠C+∠CPG=45°+∠CAG,∠CPF=∠FPG+∠CAG=45°+∠CAG,所以∠AGP=∠CPF,再由∠B=∠C,根据两角对应相等的两个三角形相似即可得△PBG∽△FCP.
试题解析:
(1)证明:如图1,
∵△ABC、△DEP是两个全等的等腰直角三角形,
∴∠B=∠C=∠DPE=45°,
∴∠BPG+∠CPF=135°,
在△BPG中,∵∠B=45°,
∴∠BPG+∠BGP=135°,
∴∠BGP=∠CPF,
∵∠B=∠C,
∴△PBG∽△FCP;
(2)△PBG与△FCP相似.理由如下:
如图2,∵△ABC、△DEP是两个全等的等腰直角三角形,
∴∠B=∠C=∠DPE=45°,
∵∠BGP=∠C+∠CPG=45°+∠CAG,
∠CPF=∠FPG+∠CAG=45°+∠CAG,
∴∠AGP=∠CPF,
∵∠B=∠C,
∴△PBG∽△FCP.


科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,BD![]() AD,延长AD至点E,使D是AE的中点,连接BE和CE,BE与CD交于点F.
AD,延长AD至点E,使D是AE的中点,连接BE和CE,BE与CD交于点F.
(1)求证:四边形BDEC是矩形;
(2)若AB=6,AD=3,求矩形BDEC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD中,AB=6 cm,BC=8 cm,点E是BC边上一点,连接AE,并将△AEB沿AE折叠,得到△AEB′,以C,E,B′为顶点的三角形是直角三角形时,BE的长为____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图反映的是小华从家里跑步去体育馆,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示小华离家的距离.根据图像回答下列问题:
(1)小华在体育馆锻炼了_____分钟;
(2)体育馆离文具店______千米;
(3)小华从家跑步到体育馆,从文具店散步回家的速度分别是多少千米/分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为边在AD的右侧作正方形ADEF,连接CF.
(1)观察猜想:如图(1),当点D在线段BC上时,
①BC与CF的位置关系是: ;
②BC、CD、CF之间的数量关系为: (将结论直接写在横线上)
(2)数学思考:如图(2),当点D在线段CB的延长线上时,上述①、②中的结论是否仍然成立?若成立,请给予证明,若不成立,请你写出正确结论再给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:(1)相反数是本身的数是正数;(2)两数相减,差小于被减数;(3)绝对值等于它相反数的数是负数;(4)倒数是它本身的数是1;(5)若![]() ,则a=b;(6)没有最大的正数,但有最大的负整数.其中正确的个数( )
,则a=b;(6)没有最大的正数,但有最大的负整数.其中正确的个数( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市质量技术监督局从某食品厂生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,把超过或不足的部分分别用正、负数来表示,记录如下表:

(1)若标准质量为450克,则抽样检测的20袋食品的总质量为多少克?
(2)若该种食品的合格标准为450±5g,求该食品的抽样检测的合格率.
查看答案和解析>>
科目:初中数学 来源: 题型:
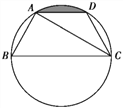
【题目】如图,已知点A,B,C,D均在已知圆上,AD∥BC,CA平分∠BCD,∠ADC=120°,四边形ABCD的周长为10.
(1)求此圆的半径;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
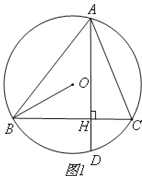
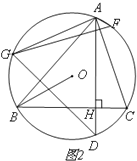
【题目】如图,△ABC内接于⊙O,弦AD⊥BC,垂足为H,连接OB.
(1)如图1,求证:∠DAC=∠ABO;
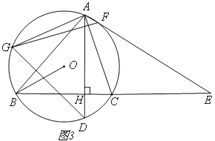
(2)如图2,在弧AC上取点F,使∠CAF=∠BAD,在弧AB取点G,使AG∥OB,若∠BAC=600,
求证:GF=GD;
(3)如图3,在(2)的条件下,AF、BC的延长线相交于点E,若AF:FE=1:9,求sin∠ADG的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com