
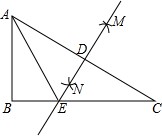
 如图,在Rt△ABC中,∠B=90°,分别以点A、C为圆心,大于$\frac{1}{2}$AC长为半径画弧,两弧相交于点M、N,作直线MN分别交AC、BC于点D、E,连结AE,若AB=3,AC=5,则BE的长为$\frac{7}{8}$.
如图,在Rt△ABC中,∠B=90°,分别以点A、C为圆心,大于$\frac{1}{2}$AC长为半径画弧,两弧相交于点M、N,作直线MN分别交AC、BC于点D、E,连结AE,若AB=3,AC=5,则BE的长为$\frac{7}{8}$.  口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:解答题
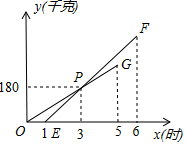 某家装公司聘请两队搬运工来搬运货物,他们都只能连续搬运5小时,甲队于某日0时开始搬运,过了1小时,乙队也开始搬运,如图,线段OG表示甲队搬运量y(千克)与时间x(时)的函数图象,线段EF表示乙队搬运量y(千克)与时间x(时)的函数图象.
某家装公司聘请两队搬运工来搬运货物,他们都只能连续搬运5小时,甲队于某日0时开始搬运,过了1小时,乙队也开始搬运,如图,线段OG表示甲队搬运量y(千克)与时间x(时)的函数图象,线段EF表示乙队搬运量y(千克)与时间x(时)的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com