
【题目】对于数轴上的点P,Q,给出如下定义:若点P到点Q的距离为d(d≥0),则称d为点P到点Q的d追随值,记作d[PQ].例如,在数轴上点P表示的数是2,点Q表示的数是5,则点P到点Q的d追随值为d[PQ]=3.
问题解决:
(1)点M,N都在数轴上,点M表示的数是1,且点N到点M的d追随值d[MN]=a(a≥0),则点N表示的数是_____(用含a的代数式表示);
(2)如图,点C表示的数是1,在数轴上有两个动点A,B都沿着正方向同时移动,其中A点的速度为每秒3个单位,B点的速度为每秒1个单位,点A从点C出发,点B表示的数是b,设运动时间为t(t>0).
①当b=4时,问t为何值时,点A到点B的d追随值d[AB]=2;
②若0<t≤3时,点A到点B的d追随值d[AB]≤6,求b的取值范围.

【答案】(1)1+a或1-a;(2)![]() 或
或![]() ;(3)1≤b≤7.
;(3)1≤b≤7.
【解析】
(1)根据d追随值的定义,分点N在点M左侧和点N在点M右侧两种情况,直接写出答案即可;
(2)①分点A在点B左侧和点A在点B右侧两种情况,类比行程问题中的追及问题,根据“追及时间=追及路程÷速度差”计算即可;②
解:(1)点N在点M右侧时,点N表示的数是1+a;
点N在点M左侧时,点N表示的数是1-a;
(2)①b=4时,AB相距3个单位,
当点A在点B左侧时,t=(3-2)÷(3-1)=![]() ,
,
当点A在点B右侧时,t=(3+2)÷(3-1)=![]() ;
;
②当点B在点A左侧或重合时,即d≤1时,随着时间的增大,d追随值会越来越大,
∵0<t≤3,点A到点B的d追随值d[AB]≤6,
∴1-d+3×(3-1)≤6,
解得d≥1,
∴d=1,
当点B在点A右侧时,即d>1时,在AB重合之前,随着时间的增大,d追随值会越来越小,
∵点A到点B的d追随值d[AB]≤6,∴d≤7
∴1<d≤7,
综合两种情况,d的取值范围是1≤d≤7.
故答案为:(1)1+a或1-a;(2)①![]() 或
或![]() ;②1≤b≤7.
;②1≤b≤7.


科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA.
(1)求证:∠BAD=∠EDC;
(2)作出点E关于直线BC的对称点M,连接DM、AM,猜想DM与AM的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,为厉行节能减排,倡导绿色出行,某公司拟在我市甲、乙两个街道社区投放一批共享单车(俗称“小黄车”),这批自行车包括A、B两种不同款型.
成本单价 (单位:元) | 投放数量 (单位:辆) | 总价(单位:元) | |
A型 | x | 50 | 50x |
B型 | x+10 | 50 |
|
成本合计(单位:元) | 7500 | ||
问题1:看表填空
如图2所示,本次试点投放的A、B型“小黄车”共有 辆;用含有x的式子表示出B型自行车的成本总价为 ;
问题2:自行车单价
试求A、B两型自行车的单价各是多少?
问题3:投放数量
现在该公司采取如下方式投放A型“小黄车”:甲街区每100人投放n辆,乙街区每100人投放(n+2)辆,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有![]() 人,求甲街区每100人投放A型“小黄车”的数量.
人,求甲街区每100人投放A型“小黄车”的数量.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯器材商场,计划用40000元从厂家购进若干部新型手机,以满足市场需求. 已知该厂家生产三种不同型号的手机,出厂价分别为:甲种型号手机每部1200元,乙种型号手机每部400元,丙种型号手机每部800元.
(1)若该商场同时购进其中两种不同型号的手机共40部,并将40000元恰好用完. 请你帮助该商场研究一下进货方案;
(2)商场每销售一部甲种型号手机可获利120元,每销售一部乙种型号手机可获利80元,每销售一部丙种型号手机可获利120元,那么在同时购进两种不同型号手机的几种方案中,哪种进货方案获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上一点,∠BOC=120°,OD平分∠AOC.
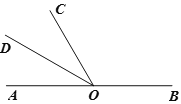
(1)求∠COD的度数.
请你补全下列解题过程.
∵点O为直线AB上一点,
∴∠AOB=_____.
∵∠BOC =120°,
∴∠AOC=______.
∵OD 平分∠AOC,
∴∠COD=![]() ∠AOC.( )
∠AOC.( )
∴∠COD=________.
(2)若E是直线AB外一点,满足∠COE:∠BOE=4:1直接写出∠BOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ABC=90°,AB=2,BC=4,现将△ABC绕顶点B顺时针方向旋转△A′BC′的位置,此时A′C′与BC的交点D是BC的中点,则线段C′D的长度是( ) 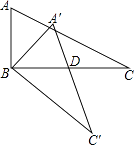
A.![]()
B.![]()
C.![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,∠A=30°.

(1)用尺规作图作AB边上的中垂线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)连接BD,求证:BD平分∠CBA.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com