

分析 (1)根据∠NOD=90°即可解决问题;
(2)①结论:∠CON-∠AOM=45°;由∠CON=90°-∠COM,∠AON=45°-∠COM,可得∠CON-∠AOM=(90°-∠COM)-(45°-∠COM)=45°
②如图3中,结论仍然成立.证明方法类似;
(3)①∠AOM=10°t,∠AOC=12°t+45°;
②由OM平分∠AOC,可得∠AOC=2∠AOM,由此列出方程12°t+45°=2•10°t,即可解决问题;
解答 解:(1)如图1中,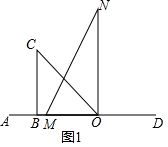
∵∠MON=∠NOD=90°,
∴t=$\frac{90}{10}$=9s.
故答案为9.
(2)①结论:∠CON-∠AOM=45°;
理由:如图2中,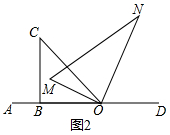
∵∠CON=90°-∠COM,∠AON=45°-∠COM,
∴∠CON-∠AOM=(90°-∠COM)-(45°-∠COM)=45°
②如图3中,结论仍然成立.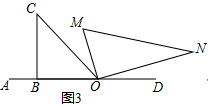
理由:∵∠CON=90°+∠COM,∠AOM=45°+∠COM,
∴∠CON-∠AOM=(90°+∠COM)-(45°+∠COM)=45°.
(3)①∠AOM=10t,∠AOC=12t+45;
②∵OM平分∠AOC,
∴∠AOC=2∠AOM,
∴12t+45°=2×10t,
解得:t=$\frac{45}{8}$,
∴当t为$\frac{45}{8}$s时OM平分∠AOC.
点评 本题考查三角形综合题、直角三角形的性质、角平分线的性质等知识,解题的关键是灵活运用所学知识解决问题,学会用构建方程的思想思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
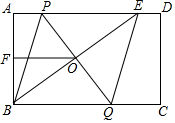 如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 组号 | ① | ② | ③ | ④ | ⑤ |
| 频数 | 8 | ■ | 15 | 10 | 11 |
| A. | 0.12 | B. | 0.6 | C. | 6 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-5,3) | B. | (-5,-1) | C. | (1,3) | D. | (1,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<4 | B. | m>1 | C. | 1<m<7 | D. | 3<m<4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x<-$\frac{1}{2}$ | B. | x$>-\frac{1}{2}$ | C. | x$<\frac{1}{2}$ | D. | x$>\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
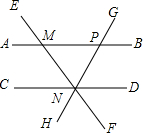 如图,直线AB∥CD,直线EF分别交AB,CD于点M,N,过点N的直线GH交AB于点P,下列结论错误的是( )
如图,直线AB∥CD,直线EF分别交AB,CD于点M,N,过点N的直线GH交AB于点P,下列结论错误的是( )| A. | ∠DNG=∠AME | B. | ∠BMN=∠MNC | C. | ∠CNH=∠BPG | D. | ∠EMB=∠END |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com