【题目】先化简,后求值
（1）(2a-3b)(3b＋2a)-（a-2b）2,其中：a=-2,b=3；
（2）［(xy+2）(xy-2)-2x2y2+4］÷(xy)，其中x=10，y=-
.
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案科目：初中数学 来源： 题型：
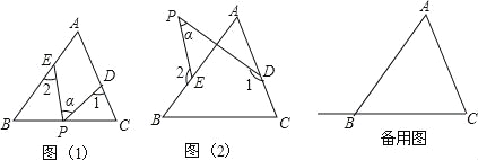
【题目】在△ABC中，∠A=50°，点D，E分别是边AC，AB上的点（不与A，B，C重合），点P是平面内一动点（P与D，E不在同一直线上），设∠PDC=∠1，∠PEB=∠2，∠DPE=∠α．
（1）若点P在边BC上运动（不与点B和点C重合），如图（1）所示，则∠1+∠2=________
（用α的代数式表示）.
（2）若点P在ABC的外部，如图（2）所示，则∠α，∠1，∠2之间有何关系？写出你的结论，并说明理由．
（3）当点P在边CB的延长线上运动时，试画出相应图形，标注有关字母与数字，并写出对应的∠α，∠1，∠2之间的关系式．（不需要证明）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在矩形ABCD中，AD=3，CD=4，点E在CD上，且DE=1．
（1）感知：如图①，连接AE，过点E作EF丄AE，交BC于点F，连接AE，易证：△ADE≌△ECF（不需要证明）；
（2）探究：如图②，点P在矩形ABCD的边AD上（点P不与点A、D重合），连接PE，过点E作EF⊥PE，交BC于点F，连接PF．求证：△PDE和△ECF相似；
（3）应用：如图③，若EF交AB于点F，EF丄PE，其他条件不变，且△PEF的面积是6，则AP的长为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图：在4×4的正方形（每个小正方形的边长均为1）网格中，以A为顶点，其他三个顶点都在格点（网格的交点）上，且面积为2的平行四边形共有多少个？( )
A.12B.16C.24D.25
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到江阴儿童福利院看望孤儿．如果分给每位儿童5盒牛奶，那么剩下18盒牛奶；如果分给每位儿童6盒牛奶，那么最后一位儿童分不到6盒，但至少能有3盒．则这个儿童福利院的儿童最少有________个，最多有________个．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有下列说法：（
）单项式
的系数、次数都是
；（
）多项式
的系数是
，它是三次二项式；（
）单项式
与
都是七次单项式；（4）单项式
和
的系数分别是
或
；（
）
是二次单项式；（
）
与
都是整式，其中正确的说法有（ ）．
A.个B. C.个D.
个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，以点C（1，1）为圆心，2为半径作圆，交x轴于A，B两点，点P在优弧
上．
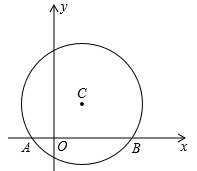
（1）求出A，B两点的坐标；
（2）试确定经过A、B且以点P为顶点的抛物线解析式；
（3）在该抛物线上是否存在一点D，使线段OP与CD互相平分？若存在，求出点D的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A(－3，2)，B(0，4)，C(0，2)．
(1)将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C；平移△ABC，若点A的对应点A2的坐标为(0，－4)，画出平移后对应的△A2B2C2；
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2，请直接写出旋转中心的坐标；
(3)在x轴上有一点P，使得PA＋PB的值最小，请直接写出点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市对当年初中升高中数学考试成绩进行抽样分析，试题满分100分，将所得成绩（均为整数）整理后，绘制了如图所示的统计图，根据图中所提供的信息，回答下列问题：
（1）共抽取了多少名学生的数学成绩进行分析？
（2）如果80分以上（包括80分）为优生，估计该年的优生率为多少？
（3）该年全市共有22000人参加初中升高中数学考试，请你估计及格（60分及60分以上）人数大约为多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
