
解:(1)过O作OE⊥AB于E,连接OA
在Rt△AEO中,∠EAO=30°
AE=

∴

∴OA=2
(2)连接CD,则∠ABC+∠ADC=180°
又∠ACB+∠ACP=180°,∠ABC=∠ACB=60°
∴∠ADC=∠ACP=120°
又∵∠CAD=∠PAC
∴△ADC∽△ACP
∴

∴AC
2=AD•AP
∴y=

=

(0<x<2

)
(3)假设D点在运动的过程中存在这样的位置,使得△DBP成为以DB,DP为腰的等腰三角形,那么DB=DP
∵∠BDC=∠BAC=60°,∠CDP=∠ABC=60°
∴∠BDC=∠CDP
∴CD⊥BP
∴DB是圆的直径,BD=4,DP=4
∵DP=AP-AD=y-x=

-x=4
即x
2+4x-12=0
∵△=42-4×(-12)=64>0
∴关于x的方程x
2+4x-12=0有两个不相等的实根,说明假设成立
∴x
1=2,x
2=-6(线段不能为负,舍去)
∴D点在运动的过程中存在这样的位置:即当AD=2时,△BDP成为以BD,PD为腰的等腰三角形.
分析:(1)过O作OE⊥AB于E,连接OA,根据等边三角形的性质和垂径定理可以E是AB的中点∠EAO=30°这样解直角三角形就可以求出半径了;
(2)连接CD,利用圆内接四边形的性质可以得到∠ADC=∠ACP=120°,还有一个公共角,可以证明△ADC∽△ACP,然后利用相似三角形的性质就可以求出函数的关系式;
(3)此题是探究性题目,一般假设结论成立,然后利用已知条件进行推理,然后进行判断.这里假设D点在运动的过程中存在这样的位置,使得△DBP成为以DB,DP为腰的等腰三角形,然后根据假设结合已知条件可以得到DB是圆的直径,这样可以得到关于x的方程,解方程就可以判断假设是否成立,然后根据方程的解就求出此时AD的长.
点评:此题综合性比较强,把一元二次方程,等边三角形,相似三角形,求函数关系式等知识放在圆的背景中,利用这些知识探究,解题.对学生的要求比较高.

 的等边三角形ABC内接于⊙O,点D在
的等边三角形ABC内接于⊙O,点D在 上运动,但与A、C两点不
上运动,但与A、C两点不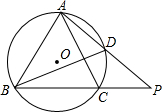 重合,连接AD并延长交BC的延长结于P.
重合,连接AD并延长交BC的延长结于P. 解:(1)过O作OE⊥AB于E,连接OA
解:(1)过O作OE⊥AB于E,连接OA


 =
= (0<x<2
(0<x<2 )
) -x=4
-x=4

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
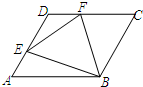 已知:如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,请你判断:无论E、F怎样移动,当满足:AE+CF=a时,△BEF是什么三角形?并说明你的结论.
已知:如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,请你判断:无论E、F怎样移动,当满足:AE+CF=a时,△BEF是什么三角形?并说明你的结论.