
【题目】已知直线AB∥CD.
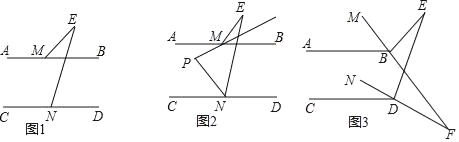
(1)如图1,直接写出∠BME、∠E、∠END的数量关系为 ;
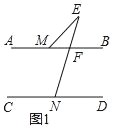
(2)如图2,∠BME与∠CNE的角平分线所在的直线相交于点P,试探究∠P与∠E之间的数量关系,并证明你的结论;
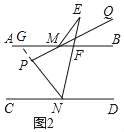
(3)如图3,∠ABM=![]() ∠MBE,∠CDN=
∠MBE,∠CDN=![]() ∠NDE,直线MB、ND交于点F,则
∠NDE,直线MB、ND交于点F,则![]() = .
= .
【答案】(1) ∠E=∠END﹣∠BME (2) ∠E+2∠NPM=180°(3)![]()
【解析】分析:(1)根据平行线的性质和三角形外角定理即可解答.
(2)根据平行线的性质,三角形外角定理,角平分线的性质即可解答.
(3)根据平行线的性质和三角形外角定理即可解答.
详解:(1)如图1,∵AB∥CD,
∴∠END=∠EFB,
∵∠EFB是△MEF的外角,
∴∠E=∠EFB﹣∠BME=∠END﹣∠BME,
(2)如图2,∵AB∥CD,
∴∠CNP=∠NGB,
∵∠NPM是△GPM的外角,
∴∠NPM=∠NGB+∠PMA=∠CNP+∠PMA,
∵MQ平分∠BME,PN平分∠CNE,
∴∠CNE=2∠CNP,∠FME=2∠BMQ=2∠PMA,
∵AB∥CD,
∴∠MFE=∠CNE=2∠CNP,
∵△EFM中,∠E+∠FME+∠MFE=180°,
∴∠E+2∠PMA+2∠CNP=180°,
即∠E+2(∠PMA+∠CNP)=180°,
∴∠E+2∠NPM=180°;
(3)如图3,延长AB交DE于G,延长CD交BF于H,
∵AB∥CD,
∴∠CDG=∠AGE,
∵∠ABE是△BEG的外角,
∴∠E=∠ABE﹣∠AGE=∠ABE﹣∠CDE,①
∵∠ABM=![]() ∠MBE,∠CDN=
∠MBE,∠CDN=![]() ∠NDE,
∠NDE,
∴∠ABM=![]() ∠ABE=∠CHB,∠CDN=
∠ABE=∠CHB,∠CDN=![]() ∠CDE=∠FDH,
∠CDE=∠FDH,
∵∠CHB是△DFH的外角,
∴∠F=∠CHB﹣∠FDH=![]() ∠ABE﹣
∠ABE﹣![]() ∠CDE=
∠CDE=![]() (∠ABE﹣∠CDE),②
(∠ABE﹣∠CDE),②
由①代入②,可得∠F=![]() ∠E,
∠E,
即![]() .
.


科目:初中数学 来源: 题型:
【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的伴随方程,这个根在数轴上对应的点该不等式组的伴随点.
(1)在方程①![]() ,②
,②![]() ,③
,③![]() 中,不等式组
中,不等式组![]() 的伴随方程是 ;(填序号)
的伴随方程是 ;(填序号)
(2)如图,M、N都是关于![]() 的不等式组
的不等式组![]() 的伴随点,求
的伴随点,求![]() 的取值范围.
的取值范围.
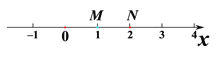
(3)不等式组![]() 的伴随方程的根有且只有2个整数,求
的伴随方程的根有且只有2个整数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店推出一种优惠卡,每张卡售价为50元,凭卡购书可享受8折优惠,小明同学到该书店购书,他先买购书卡再凭卡付款,结果省了10元。若此次小明不买卡直接购书,则他需要付款( )
A.380元B.360元C.340元D.300元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句中正确的是( )
A.两个三角形的面积相等,那么这两个三角形全等
B.三个内角对应相等的两个三角形全等
C.两个等腰直角三角形全等,那么它们的斜边相等
D.两边及其中一边所对的角对应相等的两个三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三条不同的直线a,b,c在同一平面内,下列说法正确的个数是( )
①如果a∥b,a⊥c,那么b⊥c; ②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c; ④如果b⊥a,c⊥a,那么b∥c.
A,1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com