
 如图,机器人从点A沿着西南方向行了4
如图,机器人从点A沿着西南方向行了4| 2 |
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
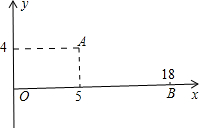 如图为机器人足球世界杯赛的一个模拟场景,直角坐标系中,原点O为球门,机器人M在点A(5,4)处发现在点B(18,0)处对方另一机器人踢的小球正向球门O作匀速直线运动,已知小球运动的速度为机器人M直线行走速度的两倍,假定机器人M与小球同时分别自A、B出发,问机器人M从点A沿直线前进,最快可在何处截住小球?并求出机器人M行走路线对应的一次函数解析式.
如图为机器人足球世界杯赛的一个模拟场景,直角坐标系中,原点O为球门,机器人M在点A(5,4)处发现在点B(18,0)处对方另一机器人踢的小球正向球门O作匀速直线运动,已知小球运动的速度为机器人M直线行走速度的两倍,假定机器人M与小球同时分别自A、B出发,问机器人M从点A沿直线前进,最快可在何处截住小球?并求出机器人M行走路线对应的一次函数解析式.查看答案和解析>>
科目:初中数学 来源: 题型:

| 2 |
| 3 |
| 5 |
| 6 |
查看答案和解析>>
科目:初中数学 来源:四川省资阳市2011年高中阶段教育学校招生考试数学试卷 题型:044
在一次机器人测试中,要求机器人从A出发到达B处.如图,已知点A在O的正西方600 cm处,B在O的正北方300 cm处,且机器人在射线AO及其右侧(AO下方)区域的速度为20 cm/秒,在射线AO的左侧(AO上方)区域的速度为10 cm/秒.
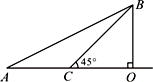
(1)分别求机器人沿A→O→B路线和沿A→B路线到达B处所用的时间(精确到秒);
(2)若∠OCB=45°,求机器人沿A→C→B路线到达B处所用的时间(精确到秒);
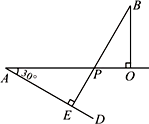
(3)如图,作∠OAD=30°,再作BE⊥AD于E,交OA于P.试说明:从A出发到达B处,机器人沿A→P→B路线行进所用时间最短.
(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,
≈1.732,![]() ≈2.236,
≈2.236,![]() ≈2.449)
≈2.449)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
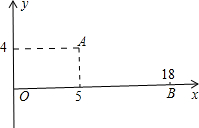 如图为机器人足球世界杯赛的一个模拟场景,直角坐标系中,原点O为球门,机器人M在点A(5,4)处发现在点B(18,0)处对方另一机器人踢的小球正向球门O作匀速直线运动,已知小球运动的速度为机器人M直线行走速度的两倍,假定机器人M与小球同时分别自A、B出发,问机器人M从点A沿直线前进,最快可在何处截住小球?并求出机器人M行走路线对应的一次函数解析式.
如图为机器人足球世界杯赛的一个模拟场景,直角坐标系中,原点O为球门,机器人M在点A(5,4)处发现在点B(18,0)处对方另一机器人踢的小球正向球门O作匀速直线运动,已知小球运动的速度为机器人M直线行走速度的两倍,假定机器人M与小球同时分别自A、B出发,问机器人M从点A沿直线前进,最快可在何处截住小球?并求出机器人M行走路线对应的一次函数解析式.查看答案和解析>>
科目:初中数学 来源:2002年安徽省普通高中理科实验班招生考试数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com