
【题目】如图,平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2). 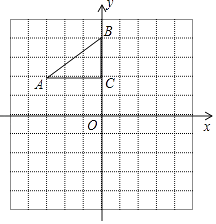
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(3)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请在坐标系中作出旋转中心S并写出旋转中心S的坐标:S
(4)在x轴上有一点P,使得PA+PB的值最小,请作图标出P点并写出点P的坐标.P .
【答案】
(1)解:如图1,△A1B1C是所求作的图形,

(2)解:如图1,平移后对应的△A2B2C2

(3)( ![]() ,﹣1)
,﹣1)
(4)(﹣2,0)
【解析】解:(3)如图1,点S是所求作的点,
由题意知,B1(0,0),B2(3,﹣2),∴S( ![]() .﹣1),
.﹣1),
所以答案是:( ![]() ,﹣1);(4)如图2,点P为所求作的点,
,﹣1);(4)如图2,点P为所求作的点,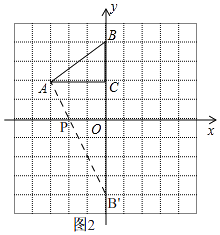
由题意,点B(0,4)与B'关于x轴对称,
∴B'(0,﹣4),
∵A(﹣3,2),
∴直线AB'的解析式为y=﹣2x﹣4,
令y=0,则﹣2x﹣4=0,
∴x=﹣2,
∴P(﹣2,0);
所以答案是(﹣2,0).
【考点精析】关于本题考查的轴对称-最短路线问题,需要了解已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径才能得出正确答案.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O逆时针方向旋转90°
得到△OA1B1 . 
(1)线段A1B1的长是 , ∠AOA1的度数是;
(2)连结AA1 , 求证:四边形OAA1B1是平行四边形;
(3)求四边形OAA1B1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在纸面上有一数轴,按要求折叠纸面:
(1)若折叠后数1对应的点与数﹣1对应的点重合,则此时数﹣3对应的点与数 对应的点重合;
(2)若折叠后数2对应的点与数﹣4对应的点重合,则此时数0对应的点与数对 应的点重合;若这样折叠后,数轴上有A、B两点也重合,且A、B两点之间的距离为11(点B在A点的右侧),则点A对应的数为 ,点B对应的数为 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】百货商店服装专柜在销售中发现:某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.为占有市场份额,在确保盈利的前提下.
(1)降价多少元时,每星期盈利为6125元.
(2)降价多少元时,每星期盈利额最大,最大盈利额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
(1)在网格中画出△A1B1C1和△A1B2C2;
(2)计算线段AC从开始变换到A1 C2的过程中扫过区域的面积(重叠部分不重复计算)
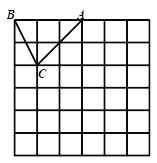
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,有一座拱桥圆弧形,它的跨度AB为60米,拱高PM为18米,当洪水泛滥到跨度只有30米时,就要采取紧急措施,若拱顶离水面只有4米,即PN=4米时,是否采取紧急措施?( ![]() =1.414)
=1.414) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=﹣1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为( ) 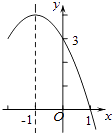
A.x=1
B.x=﹣1
C.x1=1,x2=﹣3
D.x1=1,x2=﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】未成年人思想道德建设越来越受到社会的关注,辽阳青少年研究所随机调查了本市一中学100名学生寒假中花零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观.根据调查数据制成了频
分组 | 频数 | 频率 |
0.5~50.5 |
| 0.1 |
50.5~ | 20 | 0.2 |
100.5~150.5 |
|
|
200.5 | 30 | 0.3 |
200.5~250.5 | 10 | 0.1 |
率分布表和频率分布直方图(如图).
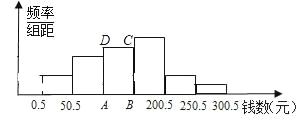
(1)补全频率分布表;
(2)在频率分布直方图中,长方形ABCD的面积是 ;这次调查的样本容量是 ;
(3)研究所认为,应对消费150元以上的学生提出勤俭节约的建议.试估计应对该校1000名学生中约多少名学生提出这项建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚为班级购买了一、二、三等奖的奖品,已知一等奖奖品6元,二等奖奖品4元,三等奖奖品2元,其中获奖人数的分配情况如图,则小刚购买奖品费用的平均数和众数分别为( )%

A. 2元,3元 B. 2.5元,2.5元 C. 3元,2元 D. 3元,3元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com