

���� ��1����CM��OB����ΪM���ɡ�ABO�ա�BCM��AO=BM=3��MC=BO=b����д����C���꣮
��2������֤����C��x���ϣ���BT=TD=a����a��ʾ�߶�AE��FC������EF=AC-AE-FC�������EF��
��3����CM��OB��GN��CM����ֱ�ΪM��N���ɡ�ABO�ա�BCM��AO=BM��BO=CM���ɡ�MOG=��GNM=��NMO=90����ı���MNGC�Ǿ��Σ��õ�MN=OG=AO=BM����NC=OM=NG�����ԡ�NGC=��NCG=45�㼴���Ƴ���OGC=135�㣬�ٸ����ı����ڽǺͶ����ó����ۣ�
��� �⣺��1��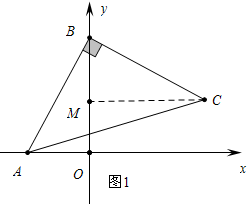 ��ͼ1����CM��OB����ΪM��
��ͼ1����CM��OB����ΪM��
�ߡ�ABC=��BMC=90�㣬
���ABO+�ϣ�MBC=90�㣬��MBC+��MCB=90�㣬
���ABO=��MCB��
�ڡ�ABO�͡�BCM�У�
$\left\{\begin{array}{l}{��AOB=��BMC=90��}\\{��ABO=��MCB}\\{AB=BC}\end{array}\right.$��
���ABO�ա�BCM��
��AO=BM=3��BO=MC=b��MO=b-3��
���C���꣨b��b-3����
��2����ͼ2����EM��AB����ΪM��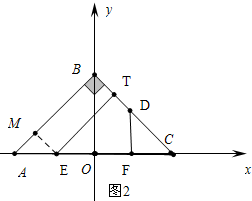 ��OA=OB=3��
��OA=OB=3��
���BAO=��ABO=45�㣬
�ߡ�ABC=90�㣬
���OBC=��BC-��ABO=45�㣬
��BA=BC����ABO=��OBC��
��AO=OC��BO��AC��
���C��x���ϣ���BT=TD=a��
�ߡ�EMB=��MBT=��BTE=90�㣬
���ı���BMET�Ǿ��Σ�
��ME=BT=a��
��RT��AME�У��ߡ�A=45�㣬ME=a��
��AE=$\sqrt{2}$ME=$\sqrt{2}$a��
��RT��DCF�У��ߡ�C=45��CD=3$\sqrt{2}$-2a��
��FG=$\frac{\sqrt{2}}{2}$CD=3-$\sqrt{2}$a��
��EF=AC-AE-FG=6-$\sqrt{2}$a-��3-$\sqrt{2}$a��=3��
��3�����ۣ���+��=135�㣬�������£�
֤������ͼ3�У�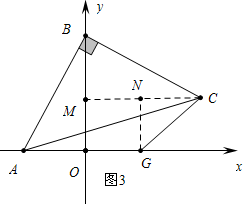 ��CM��OB��GN��CM����ֱ�ΪM��N��
��CM��OB��GN��CM����ֱ�ΪM��N��
�ɣ�1����֪��ABO�ա�BCM��
��AO=BM��BO=CM��
�ߡ�MOG=��GNM=��NMO=90�㣬
���ı���MNGC�Ǿ��Σ�
��MN=OG=AO=BM��
��NC=OM=NG��
���NGC=��NCG=45�㣬
��CM��OG��
���NGO=��GNC=90�㣬
���OGC=135�㣬
���ı���ABCG�У��ߡ�BAO+��ABC+��BCG+��AGC=360�㣬
���+��+90��+135��=360�㣬
���+��=135�㣮
���� ���⿼��ȫ�������ε��ж������ʡ�����ֱ�������ε����ʡ����ε��ж������ʵ�֪ʶ��ͨ���������߹���ȫ�������λ�����ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��ABC�͡�ADE���ǵ���ֱ�������Σ���D��AC�ϣ�MΪEC���е㣮
��ͼ����֪��ABC�͡�ADE���ǵ���ֱ�������Σ���D��AC�ϣ�MΪEC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڵȱ�������ABC�У�BD��AC���ϵ����ߣ��ӳ�BC��E��ʹCE=CD���ʣ�
��ͼ���ڵȱ�������ABC�У�BD��AC���ϵ����ߣ��ӳ�BC��E��ʹCE=CD���ʣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 һ���ӵ�������һ����ƽ�еģ��ںӵ���һ��ÿ���5����һ�������ںӵĶ�ÿ���50����һ�����߸ˣ����ⰶ�뿪����25�״����������������ڵ��������߸�ǡ�ñ��ⰶ����������ס����������������֮�仹������������ӿ���37.5m��
һ���ӵ�������һ����ƽ�еģ��ںӵ���һ��ÿ���5����һ�������ںӵĶ�ÿ���50����һ�����߸ˣ����ⰶ�뿪����25�״����������������ڵ��������߸�ǡ�ñ��ⰶ����������ס����������������֮�仹������������ӿ���37.5m���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com