
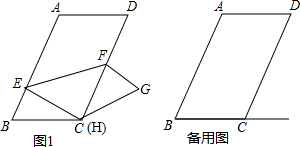
���� ��1����ͼ1�У���EP��CD��CH��AB����ֱ�ΪP��H����֤��PE=HC����RT��BCH�����CH���ɣ�
��2����ֻҪ֤����CEF=��CFE���ɣ�
����ͼ2�У�����E��EP��BC��P����PB=m����BE=2m����RT��ECP�����ù��ɶ������ɣ�
��3������ͼ3�У�����H��BC����ʱ����BE=x����RT��EPH�����ù��ɶ������ɽ������ͼ4�У�����H��BC���ӳ�����ʱ����BE=x����RT��EPH�����ù��ɶ������ɽ����
����ͼ3�У�����H��BC����ʱ����BE=x����AB��CD��$\frac{EM}{BC}$=$\frac{EH}{BH}$���г����̼��ɽ������ͼ4�У�����H��BC���ӳ�����ʱ����BE=x����AB��CD��$\frac{EM}{BC}$=$\frac{EH}{BH}$���г����̼��ɽ����
��� ��1���⣺��ͼ1�У���EP��CD��CH��AB����ֱ�ΪP��H��
���ı���ABCD��ƽ���ı��Σ�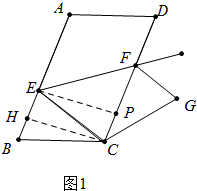
��AB��CD��
�ߡ�EPC=��EHC=90�㣬��PEH+��EPC=180��
���PEH=��EHC=��EPC=90�㣬
���ı���EHCP�Ǿ��Σ�
��EP=CH
��RT��BCH�У��ߡ�CHB=90�㣬BC=6����B=60�㣬
��BH=3��HC=$\sqrt{3}$BH=3$\sqrt{3}$��
��EP=3$\sqrt{3}$��
���E��CD�ľ���Ϊ3$\sqrt{3}$��
�ʴ�Ϊ3$\sqrt{3}$��
��2����֤������ͼ1�У����۵���֪����AEF=��CEF��
���ı���ABCD��ƽ���ı��Σ�
��AB��CD��
���AEF=��CFE��
���CEF=��CFE��
��CE=CF��
�ڽ⣺��ͼ2�У�����E��EP��BC��P��
�ߡ�EPB=90�㣬��B=60�㣬
��BE=2PB����PB=m����BE=2m��
��EP=BE•sin60��=2m•$\frac{\sqrt{3}}{2}$=$\sqrt{3}$m��
��AE=CE��AB=8��
��CF=AE=CE=8-2m��
��RT��ECP����EC2-PC2=PE2��
�ࣨ8-2m��2-��6-m��2=��$\sqrt{3}$m��2��
��m=$\frac{7}{5}$��
��PB=$\frac{7}{5}$��BE=$\frac{14}{5}$��
��CF=CE=8-2m=$\frac{26}{5}$��
��3������ͼ3�У�����H��BC����ʱ����BE=x����PB=$\frac{1}{2}$x��PE=$\frac{\sqrt{3}}{2}$x��PH=BC-CH-PB=5-$\frac{1}{2}$x��
��AE=EH=8-x��
��RT��EPH����EH2=EP2+PH2��
�ࣨ8-x��2=��$\frac{\sqrt{3}}{2}$x��2+��5-$\frac{1}{2}$X��2��
��X=$\frac{39}{11}$��
��BE=$\frac{39}{11}$��
��ͼ4�У�����H��BC���ӳ�����ʱ��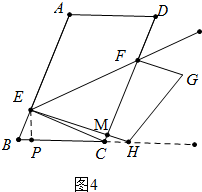 ��BE=x��
��BE=x��
��RT��EPH�У��ߡ�EPH=90�㣬EH=AE=8-x��EP=$\frac{\sqrt{3}}{2}$x��PH=7-$\frac{1}{2}$x��
�ࣨ8-x��2=��$\frac{\sqrt{3}}{2}$x��2+��7-$\frac{1}{2}$x��2��
��x=$\frac{5}{3}$��
��BE=$\frac{5}{3}$��
�൱��H��������BC�ϣ���CH=1ʱ��BE=$\frac{39}{11}$��$\frac{5}{3}$��
�ڵ���H��BC����ʱ����BE=$\frac{39}{11}$��EH=AE=8-$\frac{39}{11}$=$\frac{49}{11}$��CH=1��BH=BC-CH=5��
��AB��CD��
��$\frac{EM}{BC}$=$\frac{EH}{BH}$��
��$\frac{EM}{6}$=$\frac{\frac{49}{11}}{5}$��
��EM=$\frac{294}{55}$��
����H��BC���ӳ���ʱ����BE=$\frac{5}{3}$��EH=AE=8-$\frac{5}{3}$=$\frac{19}{3}$��CH=1��BH=BC+CH=7��
��AB��CD��
��$\frac{EM}{BC}$=$\frac{EH}{BH}$��
��$\frac{EM}{6}$=$\frac{\frac{19}{3}}{7}$��
��EM=$\frac{38}{7}$��
��EM�ij�Ϊ$\frac{294}{55}$��$\frac{38}{7}$��
���� ���⿼���ı����ۺ��⡢���۱任�����ɶ�����ƽ���߷��߶γɱ���������֪ʶ������Ĺؼ������ù��ɶ�����ƽ���߷��߶γɱ��������г����̣�����ѧ����ת��Ϊ���̽���������п��������ͣ�


 53���ò�ϵ�д�
53���ò�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У���F��BC���е㣬��E���߶�AB���ӳ����ϵ�һ���㣬����EF������C��AB��ƽ����CD�����߶�EF���ӳ��߽��ڵ�D������CE��BD��
��ͼ���ڡ�ABC�У���F��BC���е㣬��E���߶�AB���ӳ����ϵ�һ���㣬����EF������C��AB��ƽ����CD�����߶�EF���ӳ��߽��ڵ�D������CE��BD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=-6 | B�� | x=6 | C�� | x=-$\frac{6}{5}$ | D�� | x=$\frac{6}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
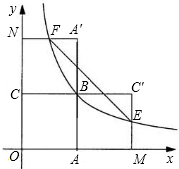 ��ͼ��������OABC�����Ϊ4������������$y=\frac{k}{x}$��x��0����ͼ����B��
��ͼ��������OABC�����Ϊ4������������$y=\frac{k}{x}$��x��0����ͼ����B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ѡ�� | �� | �� | �� | �� |
| ���� | 0.030 | 0.019 | 0.121 | 0.022 |
| A�� | �� | B�� | �� | C�� | �� | D�� | �� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com