
【题目】已知:如图,∠ABD和∠BDC的平分线交于点E,BE交CD于点F,∠1+∠2=90°.
(1)试说明:AB∥CD;
(2)试探究∠2与∠3的数量关系,并说明理由.

 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,AB边上的高CD=4,点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动,当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).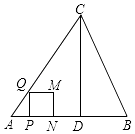
(1)直接写出tanB的值为 .
(2)求点M落在边BC上时t的值.
(3)当正方形PQMN与△ABC重叠部分为四边形时,求S与t之间的函数关系式.
(4)边BC将正方形PQMN的面积分为1:3两部分时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中.AB=AC.∠BAC=90![]() .E是AC边上的一点,延长BA至D,使AD=AE,连接DE,CD.
.E是AC边上的一点,延长BA至D,使AD=AE,连接DE,CD.
(l)图中是否存在两个三角形全等?如果存在请写出哪两个三角形全等,并且证明;如果不存在,请说明理由;
(2)若∠CBE=30![]() ,求∠ADC的度数.
,求∠ADC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑电瓶车,乙骑自行车从相距17km的两地相向而行.
(1)甲、乙同时出发经过0.5h相遇,且甲每小时行程是乙每小时行程的3倍少6km.求乙骑自行车的速度.
(2)若甲、乙骑行速度保持与(1)中的速度相同,乙先出发0.5h,甲才出发,问甲出发几小时后两人相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
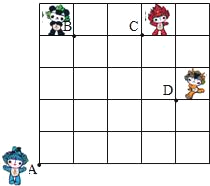
【题目】如图,奥运福娃在5×5的方格(每个格边长尾1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:
B→A(﹣4,﹣1).请根据图中所给信息解决下列问题:
(1)A→C(______),_____);
B→C(______),_____);C→_____(﹣4,﹣3);
(2)如果贝贝的行走路线为A→B→C→D,请计算贝贝走过的路程;
(3)如果贝贝从A处去寻找妮妮的行走路线依次为(+2,+2),
(+2,﹣1),(﹣2,+3),(﹣1,﹣1),请在图中标出妮妮的位置E点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,∠CAB=30°,AC=8,半径为2的⊙O从点A开始(如图1)沿直线AB向右滚动,滚动时始终与直线AB相切(切点为D),当⊙O与△ABC只有一个公共点时滚动停止,作OG⊥AC于点G. 
(1)图1中,⊙O在AC边上截得的弦长AE=;
(2)当圆心落在AC上时,如图2,判断BC与⊙O的位置关系,并说明理由. 
(3)在⊙O滚动过程中,线段OG的长度随之变化,设AD=x,OG=y,求出y与x的函数关系式,并直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知EF//AD, ∠1=∠2, ∠BAC=70°.求∠AGD的度数(将以下过程填写完整)

解:∵EF//AD
∴∠2=
又∵∠1=∠2
∴∠1=∠3
∴ AB//
∴∠BAC+ =180°.
又∵∠BAC=70°
∴∠AGD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据说,我国著名数学家华罗庚在一次访问途中,看到飞机邻座的乘客阅读的杂志上有一道智力题:一个数32768,它是一个正数的立方,希望求它的立方根,华罗庚不假思索给出了答案,邻座乘客非常惊奇,很想得知其中的奥秘,你知道华罗庚是怎样准确计算出的吗?请按照下面的问题试一试:
(1)由![]() ,因为
,因为![]() ,请确定
,请确定![]() 是______位数;
是______位数;
(2)由32768的个位上的数是8,请确定![]() 的个位上的数是________,划去32768后面的三位数768得到32,因为
的个位上的数是________,划去32768后面的三位数768得到32,因为![]() ,请确定
,请确定![]() 的十位上的数是_____________
的十位上的数是_____________
(3)已知13824和![]() 分别是两个数的立方,仿照上面的计算过程,请计算:
分别是两个数的立方,仿照上面的计算过程,请计算:![]() =____;
=____;![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以x为自变量的二次函数y=x2﹣2(b﹣2)x+b2﹣1的图象不经过第三象限,则实数b的取值范围是( )
A.b≥ ![]()
B.b≥1或b≤﹣1
C.b≥2
D.1≤b≤2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com