
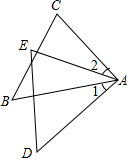
 如图,∠1=∠2,AB=AD,AC=AE.请将下面说明∠C=∠E的过程和理由补充完整.
如图,∠1=∠2,AB=AD,AC=AE.请将下面说明∠C=∠E的过程和理由补充完整. 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:解答题
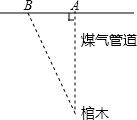 如图,一个古代棺木被探明位于A点地下24米处,由于A点地面下有煤气管道,考古人员下能垂直向下挖掘,他们被允许从距A点8米的B点挖掘,考占人员应以与地平面形成多大的角度进行挖掘才能沿最短路线挖到棺木?他们需要挖多长的距离?
如图,一个古代棺木被探明位于A点地下24米处,由于A点地面下有煤气管道,考古人员下能垂直向下挖掘,他们被允许从距A点8米的B点挖掘,考占人员应以与地平面形成多大的角度进行挖掘才能沿最短路线挖到棺木?他们需要挖多长的距离?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
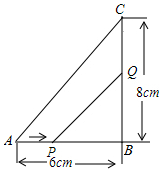 如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米.点P从A点开始沿A边向点B以1厘米/秒的速度移动(到达点B即停止运动),点Q从B点开始沿BC边向点C以2厘米/秒的速度移动(到达点C即停止运动).
如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米.点P从A点开始沿A边向点B以1厘米/秒的速度移动(到达点B即停止运动),点Q从B点开始沿BC边向点C以2厘米/秒的速度移动(到达点C即停止运动).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,等腰△ABC中,AB=AC=13,BC=10,D是BC边上任意一点,DE⊥AB于E,DF⊥AC于点F,则DE+DF=$\frac{120}{13}$.
如图,等腰△ABC中,AB=AC=13,BC=10,D是BC边上任意一点,DE⊥AB于E,DF⊥AC于点F,则DE+DF=$\frac{120}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6厘米和10厘米 | B. | 8厘米和10厘米 | C. | 6厘米和8厘米 | D. | 8厘米和8厘米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
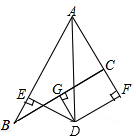 已知:如图∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
已知:如图∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com