
【题目】在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 内一点.
内一点.
(1)如图1,连接![]() ,将
,将![]() 沿射线
沿射线![]() 方向平移,得到
方向平移,得到![]() ,点
,点![]() 的对应点分别为点
的对应点分别为点![]() ,连接
,连接![]() .如果
.如果![]() ,
,![]() ,则
,则![]() .
.
(2)如图2,连接![]() ,当
,当![]() 时,求
时,求![]() 的最小值.
的最小值.

【答案】(1)![]() ;(2)2
;(2)2![]() +2
+2![]()
【解析】
(1)连接CD,构造矩形ACBD和Rt△CDE,根据矩形的对角线相等以及勾股定理进行计算,即可求得CE的长;
(2)以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接BN.根据△PAM、△ABN都是等边三角形,可得PA+PB+PC=CP+PM+MN,最后根据当C、P、M、N四点共线时,由CA=CB,NA=NB可得CN垂直平分AB,进而求得PA+PB+PC的最小值.
如图,连接CD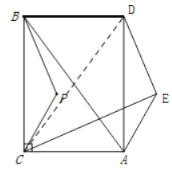
∵△BCP沿射线CA方向平移,得到△DAE,
∴BC∥AD且BC=AD,
∵∠ACB=90°,
∴四边形BCAD是矩形,
∴CD=AB=6,
∵BP=3,
∴DE=BP=3,
∵BP⊥CE,BP∥DE,
∴DE⊥CE,
∴在Rt△DCE中,CE=![]()
(2)如图所示,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接BN.那么就将PA+PB+PC的值转化为CP+PM+MN的值,连接CN,当点P落在CN上时,PA+PB+PC的值最小.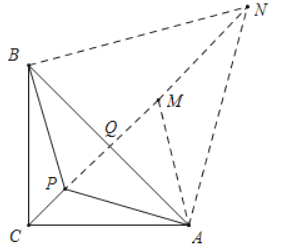
由旋转可得,△AMN≌△ABP,
∴MN=BP,PA=AM,∠PAM=60°=∠BAN,AB=AN,
∴△PAM、△ABN都是等边三角形,
∴PA=PM,
∴PA+PB+PC=CP+PM+MN,
当AC=BC=4时,AB=4![]() ,
,
当C、P、M、N四点共线时,由CA=CB,NA=NB可得CN垂直平分AB,
∴AQ=![]() AB=2
AB=2![]() =CQ,NQ=
=CQ,NQ=![]() AQ=2
AQ=2![]() ,
,
∴此时CN=CP+PM+MN=PA+PB+PC=2![]() +2
+2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,某商场为了吸引顾客,制作了可以自由转动的转盘(转盘被等分成20个扇形),顾客每购买200元的商品,就能获得一次转动转盘的机会,如果转动转盘,转盘停止后指针正好对准红色、黄色或绿色区域,就可以分别获得200元、100元、50元的购物券;如果不愿意,可直接获得30元的购物券.

(1)求转动一次转盘获得购物券的概率;
(2)如果你在该商场消费210元,你会选择转转盘还是直接获得购物券?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
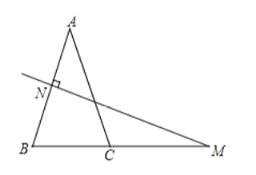
【题目】在![]() 中,
中,![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
(1)若![]() ,则
,则![]() 为 度;
为 度;
(2)如果![]() (
(![]() ),其余条件不变,求
),其余条件不变,求![]() 的度数;
的度数;
(3)补全规律:等腰三角形一腰的垂直平分线与 相交所成的锐角等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E为AB边上一点,EC平分∠DEB,F为CE的中点,连接AF,BF,过点E作EH∥BC分别交AF,CD于G,H两点. 
(1)求证:DE=DC;
(2)求证:AF⊥BF;
(3)当AFGF=28时,请直接写出CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),A(0,1)是正方形![]() 的两个顶点,以
的两个顶点,以![]() 对角线为边作正方形
对角线为边作正方形![]() ,再以正方形的对角线
,再以正方形的对角线![]() 作正方形
作正方形![]() ,…,依此规律,则点
,…,依此规律,则点![]() 的坐标是( )
的坐标是( )

A. (-8,0) B. (0,8)
C. (0,8![]() ) D. (0,16)
) D. (0,16)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC. 
(1)求证:四边形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣1,1)、B(4,6)在抛物线y=ax2+bx上
(1)求抛物线的解析式;
(2)如图1,点F的坐标为(0,m)(m>2),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H.设抛物线与x轴的正半轴交于点E,连接FH、AE,求证:FH∥AE;
(3)如图2,直线AB分别交x轴、y轴于C、D两点.点P从点C出发,沿射线CD方向匀速运动,速度为每秒 ![]()
个单位长度;同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度.点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=2PM,直接写出t的值.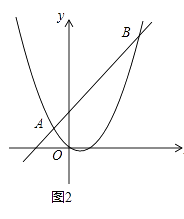
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com