
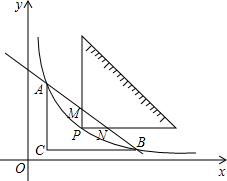
 ��ͼ����һ��ֱ��������ֽ���ֱ�Ƕ������C��1��$\frac{1}{2}$��������ֱ�DZ߷ֱ���x��y��ƽ�У�ֽ�������������A��Bǡ����ֱ��y=kx+b��˫����y=$\frac{4}{x}$�Ľ��㣮
��ͼ����һ��ֱ��������ֽ���ֱ�Ƕ������C��1��$\frac{1}{2}$��������ֱ�DZ߷ֱ���x��y��ƽ�У�ֽ�������������A��Bǡ����ֱ��y=kx+b��˫����y=$\frac{4}{x}$�Ľ��㣮���� ��1���ȵõ�A��ĺ�����Ϊ1��B���������Ϊ$\frac{1}{2}$�������÷���������ͼ���ϵ�������������A��1��4����B��8��$\frac{1}{2}$����Ȼ�����ô���ϵ�������һ�κ�������ʽ���Ӷ��õ�k��b��ֵ��
��2��������ڵ�Pʹ��MN=$\frac{1}{2}$AB��ֱ��AB�Ľ���ʽΪy=-$\frac{1}{2}$x+$\frac{9}{2}$����֤��Rt��PMN��Rt��CAB�õ�$\frac{PM}{AC}$=$\frac{PN}{BC}$=$\frac{MN}{AB}$=$\frac{1}{2}$����P��x��$\frac{4}{x}$������1��x��8������M��x��-$\frac{1}{2}$x+$\frac{9}{2}$������MP=-$\frac{1}{2}$x+$\frac{9}{2}$-$\frac{4}{x}$������2��-$\frac{1}{2}$x+$\frac{9}{2}$-$\frac{4}{x}$��=$\frac{7}{2}$��������2x2-11x+16=0�������б�ʽ�������жϷ���û��ʵ���⣬���Բ����ڵ�Pʹ��MN=$\frac{1}{2}$AB��
��3������Rt��PMN��Rt��CAB�õ�$\frac{{S}_{��PMN}}{{S}_{��ABC}}$=��$\frac{-\frac{1}{2}x+\frac{9}{2}-\frac{4}{x}}{\frac{7}{2}}$��2����S��ABC=$\frac{49}{4}$������S��PMN=��$\frac{9}{2}$-$\frac{1}{2}$x-$\frac{4}{x}$��2�����ò���ʽ��ʽ��$\frac{1}{2}$x+$\frac{4}{x}$��2$\sqrt{2}$�����Ե�x=2$\sqrt{2}$ʱ��$\frac{1}{2}$x+$\frac{4}{x}$����Сֵ����ʱS��PMN�����ֵ��Ȼ��ѵ�x=2$\sqrt{2}$������㼴�ɵõ�S��PMN�����ֵ=$\frac{113-72\sqrt{2}}{4}$����ʱP������Ϊ��2$\sqrt{2}$��$\sqrt{2}$����
��� �⣺��1����AC��y�ᣬBC��x�ᣬ
��C��1��$\frac{1}{2}$����
��A��ĺ�����Ϊ1��B���������Ϊ$\frac{1}{2}$��
�ߵ�A��B��˫����y=$\frac{4}{x}$�ϣ�
��A��1��4����B��8��$\frac{1}{2}$����
�ߵ�A��B��ֱ��y=kx+b�ϣ�
��$\left\{\begin{array}{l}{k+b=4}\\{8k+b=\frac{1}{2}}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=\frac{9}{2}}\end{array}\right.$��
��2�������ڵ�Pʹ��MN=$\frac{1}{2}$AB���������£�
������ڵ�Pʹ��MN=$\frac{1}{2}$AB��ֱ��AB�Ľ���ʽΪy=-$\frac{1}{2}$x+$\frac{9}{2}$��
��PM��y�ᣬAC��y�ᣬ
��PM��AC��
���PMN=��BAC��
��Rt��PMN��Rt��CAB��
��$\frac{PM}{AC}$=$\frac{PN}{BC}$=$\frac{MN}{AB}$=$\frac{1}{2}$��
��P��x��$\frac{4}{x}$������1��x��8������M��x��-$\frac{1}{2}$x+$\frac{9}{2}$����
��MP=-$\frac{1}{2}$x+$\frac{9}{2}$-$\frac{4}{x}$��
��AC=4-$\frac{1}{2}$=$\frac{7}{2}$��
��2��-$\frac{1}{2}$x+$\frac{9}{2}$-$\frac{4}{x}$��=$\frac{7}{2}$��
������2x2-11x+16=0��
�ߡ�=��-11��2-4��2��16=-7��0
���û��ʵ���⣬
����ڵ�Pʹ��MN=$\frac{1}{2}$AB��
��3����MPN ������������ֵ��
��Rt��PMN��Rt��CAB��
��$\frac{{S}_{��PMN}}{{S}_{��ABC}}$=��$\frac{PM}{AC}$��2=��$\frac{-\frac{1}{2}x+\frac{9}{2}-\frac{4}{x}}{\frac{7}{2}}$��2��
��S��ABC=$\frac{1}{2}$•$\frac{7}{2}$•��8-1��=$\frac{49}{4}$��
��S��PMN=��$\frac{9}{2}$-$\frac{1}{2}$x-$\frac{4}{x}$��2��
��$\frac{1}{2}$x+$\frac{4}{x}$��2$\sqrt{\frac{1}{2}x•\frac{4}{x}}$����$\frac{1}{2}$x+$\frac{4}{x}$��2$\sqrt{2}$��
�൱$\frac{1}{2}$x=$\frac{4}{x}$ʱ����x=2$\sqrt{2}$ʱ��$\frac{1}{2}$x+$\frac{4}{x}$����Сֵ��
��ʱS��PMN�����ֵ��
��x=2$\sqrt{2}$ʱ��S��PMN�����ֵ=$\frac{113-72\sqrt{2}}{4}$����ʱP������Ϊ��2$\sqrt{2}$��$\sqrt{2}$����
���� ���⿼���˷������������ۺ��⣺�������շ���������ͼ���ϵ������������һ�κ���ͼ���ϵ�����������������ô���ϵ������������ʽ�����������������ε��������߶κ������ε��������ס����ʽa+b��2$\sqrt{ab}$��a��bΪ��������a=bʱȡ�Ⱥţ���


 ��������ϵ�д�
��������ϵ�д� ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д� ��ѧ�����ϵ�д�
��ѧ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����һ��������ֽ�е�չ��ͼ��������������������A��B��C�зֱ������ʵ�������ʹ�������۳����������Ե�������������Ϊ�෴����������������A��B��C�е������������ǣ�������
��ͼ����һ��������ֽ�е�չ��ͼ��������������������A��B��C�зֱ������ʵ�������ʹ�������۳����������Ե�������������Ϊ�෴����������������A��B��C�е������������ǣ�������| A�� | -3��$-\frac{1}{2}$��1 | B�� | $-\frac{1}{2}$��-3��1 | C�� | 1��-3��$-\frac{1}{2}$ | D�� | -3��1��$-\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=-2x | B�� | y=$\frac{2}{x}$ | C�� | y=2x-1 | D�� | y=-x2+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
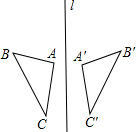 ��ͼ����ABC���A��B��C�����ֱ��l�Գƣ���A=98�㣬��C��=28�㣬���B�Ķ���Ϊ��������
��ͼ����ABC���A��B��C�����ֱ��l�Գƣ���A=98�㣬��C��=28�㣬���B�Ķ���Ϊ��������| A�� | 28�� | B�� | 54�� | C�� | 74�� | D�� | 78�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
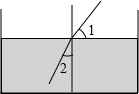 ��ͼ�������ߴӿ�������ˮ��ʱ�����ߵĴ����������˸ı䣬�������������ͼ�С�1=47�㣬��2=30�㣬���Ĵ�������ı�Ķ���Ϊ��������
��ͼ�������ߴӿ�������ˮ��ʱ�����ߵĴ����������˸ı䣬�������������ͼ�С�1=47�㣬��2=30�㣬���Ĵ�������ı�Ķ���Ϊ��������| A�� | 13�� | B�� | 15�� | C�� | 17�� | D�� | 19�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ԴP��ˮƽ���õĺ��AB�����Ϸ���AB�ڵƹ��µ�Ӱ��CDҲ��ˮƽ״̬��AB=2m��CD=6m����P��CD�ľ�����3.9m����AB��CD֮��ľ����ǣ�������
��ͼ����ԴP��ˮƽ���õĺ��AB�����Ϸ���AB�ڵƹ��µ�Ӱ��CDҲ��ˮƽ״̬��AB=2m��CD=6m����P��CD�ľ�����3.9m����AB��CD֮��ľ����ǣ�������| A�� | 2.6m | B�� | 2m | C�� | 1.3m | D�� | 1m |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com