下列调查中应选择普查的是( )A．日光灯管厂要检测一批灯管的使用寿命B．了解嘉兴市每天的流动人口数C．了解浙江省城市居民日平均用水量D．旅客上飞机前的安全检查题目和参考答案——青夏教育精英家教网—

7．下列调查中应选择普查的是（　　）

	A．	日光灯管厂要检测一批灯管的使用寿命
	B．	了解嘉兴市每天的流动人口数
	C．	了解浙江省城市居民日平均用水量
	D．	旅客上飞机前的安全检查

分析由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似．

解答解：A、要了解日光灯管厂要检测一批灯管的使用寿命，由于破坏性较强，应采用抽样调查方式，故A选项错误；
B、要了解嘉兴市每天的流动人口数，由于范围较大，采用抽样调查方式，故B选项错误；
C、要了解浙江省城市居民日平均用水量，由于范围较大，采用抽查方式，故C选项错误；
D、旅客上飞机前的安全检查，应采用普查的方式，故D选项正确；
故选：D．

点评本题考查了抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．

练习册系列答案

品至教育假期复习计划期末寒假衔接系列答案

假期园地寒假系列答案

假期生活寒假花山文艺出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：选择题

17．以下四个标志图案是轴对称图形的是（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

18．（1）知识再现
如图（1）：若点A，B在直线l同侧，A，B到l的距离分别是3和2，AB=4，现在直线l上找一点P，使AP+BP的值最小．作法如下；作点A关于直线l的对称点A′，连接BA′，与直线l的交点就是所求的点P，线段BA′的长度即为AP+BP的最小值，请你求出这个最小值．
（2）实践应用
①如图（2），⊙O的半径为2，点A、B、C在⊙O上，OA⊥OB，∠AOC=60°，P是OB上一动点，则PA+PC的最小值是2$\sqrt{3}$；
②如图（3），Rt△OAB的顶点A在x轴的正半轴上，顶点B的坐标为（3，$\sqrt{3}$），点C的坐标为（1，0），点P为斜边OB上的一动点，则PA+PC的最小值为$\sqrt{7}$；
③如图（4），菱形ABCD中AB=2，∠A=120°，点P，Q，K，分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为2；
④如图（5），在Rt△ABC中，∠C=90°，∠B=60°，点D是BC边上的点，CD=$\sqrt{3}$，将△ABC沿直线AD翻折，使点C落在AB边上的点E处，若点P是直线AD上的动点，则△PEB的周长的最小值是3+$\sqrt{3}$．
（3）拓展延伸
如图（6），在四边形ABCD的对角线AC上找一点P，使∠APB=∠APD，保留作图痕迹，不必写出作法．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

15．用长度均为m的绳子分别围成下列四种图形，无论m取何值时，面积最大的是（　　）

A．

等边三角形

B．

正方形

C．

正六边形

D．

圆

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

2．

如图，六边形ABCDEF是正六边形，曲线FK₁K₂K₃K₄K₅K₆K₇…叫做“正六边形的渐开线”，其中$\widehat{F{K}_{1}}$，$\widehat{{K}_{1}{K}_{2}}$，$\widehat{{K}_{2}{K}_{3}}$，$\widehat{{K}_{3}{K}_{4}}$，$\widehat{{K}_{4}{K}_{5}}$…的圆心依次按点A，B，C，D，E，F循环，分别记为l₁，l₂，l₃，l₄，l₅，l₆…当AB=1时，l₂₀₁₂等于$\frac{2012π}{3}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

12．

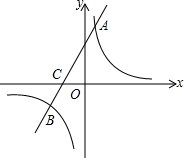如图，在平面直角坐标系中，一次函数y=2x+b的图象与反比例函数y=$\frac{k}{x}$（k≠0）的图象交于A、B两点，与x轴交于点C（-2，0），点A的坐标为（n，6）．
（1）求该反比例函数的解析式；
（2）求点B的坐标，写出一次函数值大于反比例函数值时自变量x的取值范围；
（3）若点E为x轴上使△ACE为直角三角形的一点，求点E的坐标．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

19．