
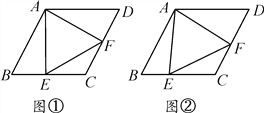
【题目】菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图①,若点E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)首先连接AC,由菱形ABCD中,∠B=60°,根据菱形的性质,易得△ABC是等边三角形,又由三线合一,可证得AE⊥BC,继而求得∠FEC=∠CFE,即可得EC=CF,继而证得BE=DF;
(2)首先由△ABC是等边三角形,即可得AB=AC,以求得∠ACF=∠B=60°,然后利用平行线与三角形外角的性质,可求得∠AEB=∠AFC,证得△AEB≌△AFC,即可得AE=AF,证得:△AEF是等边三角形.
试题解析:(1)连接AC,
∵在菱形ABCD中,∠B=60°,
∴AB=BC=CD,∠C=180°-∠B=120°,
∴△ABC是等边三角形,
∵E是BC的中点,
∴AE⊥BC,
∵∠AEF=60°,
∴∠FEC=90°-∠AEF=30°,
∴∠CFE=180°-∠FEC-∠ECF=180°-30°-120°=30°,
∴∠FEC=∠CFE,
∴EC=CF,
∴BE=DF;
(2)∵△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
∴∠B=∠ACF=60°,
∵AD∥BC,
∴∠AEB=∠EAD=∠EAF+∠FAD=60°+∠FAD,
∠AFC=∠D+∠FAD=60°+∠FAD,
∴∠AEB=∠AFC,
在△ABE和△ACF中,
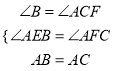
∴△ABE≌△ACF(AAS),
∴AE=AF,
∵∠EAF=60°,
∴△AEF是等边三角形.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】如图,有一张边长为6的正方形纸片ABCD,P是AD边上一点(不与点A、D重合),将正方形纸片沿EF折叠,使点B落在点P处,点C落在点G处,PG交DC于H,连接BP.
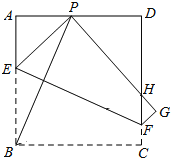
(1)求证:∠APB=∠BPH;
(2)若P为AD中点,求四边形EFGP的面积;
(3)当点P在边AD上移动时,△PDH的周长是否发生变化?写出你的结论并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形![]() 为正方形,点
为正方形,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() ,过点
,过点![]() 作
作![]() ,交射线
,交射线![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() ,连接
,连接![]() .
.
(1)如图,求证:矩形![]() 是正方形;
是正方形;

(2)当线段![]() 与正方形
与正方形![]() 的某条边的夹角是
的某条边的夹角是![]() 时,求
时,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
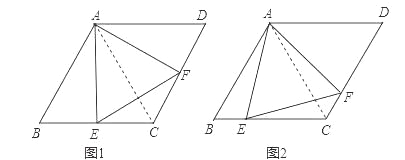
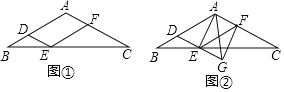
【题目】如图①,在△ABC中,AB=AC,过AB上一点D作DE∥AC交BC于点E,以E为顶点,ED为一边,作∠DEF=∠A,另一边EF交AC于点F.
(1)求证:四边形ADEF为平行四边形;
(2)当点D为AB中点时,判断ADEF的形状;
(3)延长图①中的DE到点G,使EG=DE,连接AE,AG,FG,得到图②,若AD=AG,判断四边形AEGF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级(1)班要从班级里数学成绩较优秀的甲、乙两位学生中选拔一人参加“全国初中数学联赛”,为此,数学老师对两位同学进行了辅导,并在辅导期间测验了6次,测验成绩如下表(单位:分):
次数,1, 2, 3, 4, 5, 6
甲:79,78,84,81,83,75
乙:83,77,80,85,80,75
利用表中数据,解答下列问题:
(1)计算甲、乙测验成绩的平均数.
(2)写出甲、乙测验成绩的中位数.
(3)计算甲、乙测验成绩的方差.(结果保留小数点后两位)
(4)根据以上信息,你认为老师应该派甲、乙哪名学生参赛?简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A![]() ,B(-1,2)是一次函数
,B(-1,2)是一次函数![]() 与反比例函数
与反比例函数![]()
(![]() )图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
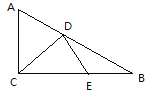
【题目】在Rt△ABC中,∠ACB=90°,AC=4,BC=8,D,E是AB和BC上的动点,连接CD,DE则CD+DE的最小值为( )
A. 8 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 上有一点
上有一点![]() ,过
,过![]() 作射线
作射线![]() ,嘉琪将一直角三角板的直角顶点与
,嘉琪将一直角三角板的直角顶点与![]() 重合.
重合.

(1)嘉琪把三角板![]() 如图1放置,若
如图1放置,若![]() ,则
,则![]() ,
,![]() ;
;
(2)嘉琪将直角三角板绕![]() 点顺时针旋转一定角度后如图2,使
点顺时针旋转一定角度后如图2,使![]() 平分
平分![]() ,且
,且![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com