
���� �٢��ɵ�ʽ���Կ���������1����ĸ���������������ij˻������Բ��������������Ϊ��ĸ��������1�����������IJ��$\frac{1}{2}$���ɴ˹��ɵó��𰸼��ɣ�
�۴���ʽ�ӣ���ֺ���㼴�ɣ�
��ͨ���۵Ľ�����֣���ӵ���Խ�࣬��ֵԽ��Խ�����Խ��Խ�ӽ�$\frac{1}{2}$��
��� �⣺�١ߵ�1����ʽ��a1=$\frac{1}{1��3}$=$\frac{1}{2}$����1-$\frac{1}{3}$����
��2����ʽ��a2=$\frac{1}{3��5}$=$\frac{1}{2}$����$\frac{1}{3}$-$\frac{1}{5}$����
��3����ʽ��a3=$\frac{1}{5��7}$=$\frac{1}{2}$����$\frac{1}{5}$-$\frac{1}{7}$����
��4����ʽ��a4=$\frac{1}{7��9}$=$\frac{1}{2}$����$\frac{1}{7}$-$\frac{1}{9}$����
���5����ʽ��a5=$\frac{1}{9��11}$=$\frac{1}{2}$����$\frac{1}{9}$-$\frac{1}{11}$����
�ڵ�n����ʽ��an=$\frac{1}{��2n-1����2n+1��}$=$\frac{1}{2}$����$\frac{1}{2n-1}$-$\frac{1}{2n+1}$����
��a1+a2+a3+a4+��+a2015
=$\frac{1}{1��3}$+$\frac{1}{3��5}$+$\frac{1}{5��7}$+��+$\frac{1}{4029��4031}$
=$\frac{1}{2}$����1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+��+$\frac{1}{4029}$-$\frac{1}{4030}$��
=$\frac{1}{2}$��$\frac{4029}{4030}$
=$\frac{4029}{8060}$��
�ܵ�n��������ʱ��a1+a2+a3+a4+��+an���ӽ�$\frac{1}{2}$��
��Ϊ��ȡ$\frac{1}{2}$�������ڵ�����1-$\frac{1}{2n+1}$Խ��Խ�ӽ�1��
���Ե�n��������ʱ�����ӽ�$\frac{1}{2}$��
���� ���⿼�����ֵı仯���ɣ��ҳ�����֮���������ɣ����������ֵı仯�����ñ仯�Ĺ��ɽ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
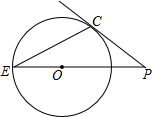 ��ͼ����PΪ��0��һ�㣬PC���0�����ڵ�C��PO���ӳ��߽���0��E����0�İ뾶Ϊ3��PC=4����CE�ij���
��ͼ����PΪ��0��һ�㣬PC���0�����ڵ�C��PO���ӳ��߽���0��E����0�İ뾶Ϊ3��PC=4����CE�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
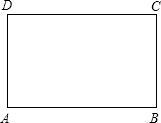 ��ͼ�����ε��ܳ�Ϊ20������
��ͼ�����ε��ܳ�Ϊ20�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{5}$ | B�� | $\frac{5}{3}$ | C�� | $\frac{3}{4}$ | D�� | $\frac{4}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
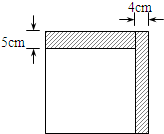 ��ͼ��С����һ�������ε�ֽƬ��ȥһ����Ϊ4cm�ij������ٴ�ʣ�µij�����ֽƬ�ϼ�ȥһ����Ϊ5cm�ij����������μ��µ��������������������ȣ������ʣ�µ�ͼ�ε������
��ͼ��С����һ�������ε�ֽƬ��ȥһ����Ϊ4cm�ij������ٴ�ʣ�µij�����ֽƬ�ϼ�ȥһ����Ϊ5cm�ij����������μ��µ��������������������ȣ������ʣ�µ�ͼ�ε�������鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com