
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
 已知:如图,在梯形ABCD中,AD∥BC,AB=DC,点E、F、G分别在边AB、BC、CD上,AE=GF=GC
已知:如图,在梯形ABCD中,AD∥BC,AB=DC,点E、F、G分别在边AB、BC、CD上,AE=GF=GC 查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 定义:如图,点M、N把线段AB分割成AM、MN和BN,若以AM、MN、BN为边的三角形构成一个直角三角形,则称点M、N是线段AB的勾股分割点,若AM=2,MN=3,则BN的长为( )
定义:如图,点M、N把线段AB分割成AM、MN和BN,若以AM、MN、BN为边的三角形构成一个直角三角形,则称点M、N是线段AB的勾股分割点,若AM=2,MN=3,则BN的长为( )| A. | $\sqrt{5}$ | B. | $\sqrt{13}$ | C. | $\sqrt{5}$或$\sqrt{13}$ | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
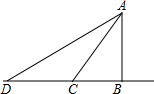 如图,某学校A与直线公路BD的距离AB为3km,与该公路上一车站D相距5km,现要在公路边建一个小商店C,使之与学校A及车站D的距离相等,请你推算一下,该商店应建在距车站D多远处.
如图,某学校A与直线公路BD的距离AB为3km,与该公路上一车站D相距5km,现要在公路边建一个小商店C,使之与学校A及车站D的距离相等,请你推算一下,该商店应建在距车站D多远处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com