
【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).

(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移![]() 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
【答案】(1)y=![]() ;(2)﹣1<x<0或x>1;(3)见解析
;(2)﹣1<x<0或x>1;(3)见解析
【解析】
试题分析:(1)设反比例函数的解析式为y=![]() (k>0),然后根据条件求出A点坐标,再求出k的值,进而求出反比例函数的解析式;
(k>0),然后根据条件求出A点坐标,再求出k的值,进而求出反比例函数的解析式;
(2)直接由图象得出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)首先求出OA的长度,结合题意CB∥OA且CB=![]() ,判断出四边形OABC是平行四边形,再证明OA=OC即可判定出四边形OABC的形状.
,判断出四边形OABC是平行四边形,再证明OA=OC即可判定出四边形OABC的形状.
解:(1)设反比例函数的解析式为y=![]() (k>0),
(k>0),
∵A(m,﹣2)在y=2x上,
∴﹣2=2m,
∴m=﹣1,
∴A(﹣1,﹣2),
又∵点A在y=![]() 上,
上,
∴k=2,
∴反比例函数的解析式为y=![]() ;
;
(2)观察图象可知正比例函数值大于反比例函数值时自变量x的取值范围为﹣1<x<0或x>1;
(3)四边形OABC是菱形.
证明:∵A(﹣1,﹣2),
∴OA=![]() =
=![]() ,
,
由题意知:CB∥OA且CB=![]() ,
,
∴CB=OA,
∴四边形OABC是平行四边形,
∵C(2,n)在y=![]() 上,
上,
∴n=1,
∴C(2,1),
OC=![]() =
=![]() ,
,
∴OC=OA,
∴四边形OABC是菱形.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】(请在括号里注明重要的推理依据)
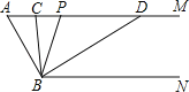
如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知P(﹣3,m)和 Q(1,m)是抛物线y=x2+bx﹣3上的两点.

(1)求b的值;
(2)将抛物线y=x2+bx﹣3的图象向上平移k(是正整数)个单位,使平移后的图象与x轴无交点,求k的最小值;
(3)将抛物线y=x2+bx﹣3的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合新图象回答:当直线y=x+n与这个新图象有两个公共点时,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.

(1)求证:AB=BE;
(2)若PA=2,cosB=![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则:①∠ABO的度数是 ;
②如图2,当∠BAD=∠ABD时,试求x的值(要说明理由);
(2)如图3,若AB⊥OM,则是否存在这样的X的值,使得△ADB中有两个相等的角?若存在,直接写出x的值;若不存在,说明理由.(自己画图)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校举办歌咏比赛,7位评委给某一位选手的平分不尽相同,若去掉一个最高分,去掉一个最低分,则下列统计量一定会发生变化的是( )
A. 方差 B. 平均数 C. 众数 D. 中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一个图案上各个点的横坐标和纵坐标分别加正数a,则所得的图案与原来图案相比( )
A.形状不变,大小扩大到原来的a倍
B.图案向右平移了a个单位
C.图案向上平移了a个单位
D.图案向右平移了a个单位,并且向上平移了a个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com