

分析 (1)在Rt△OAB中,已知了OB=12cm,∠0AB=30°,即可求出线段AB、OA的长度;
(2)连接O′M,当PM与⊙O′相切时,PM、PO同为⊙O′的切线,易证得△OO′P≌△MO′P,则∠OO′P=∠MO′P;在(1)中易得∠OBA=60°,即△O′BM是等边三角形,由此可得到∠BO′M=∠PO′M=∠PO′O=60°;在Rt△OPO′中,根据∠PO′O的度数及OO′的长即可求得OP的长,已知了P点的运动速度,即可根据时间=路程÷速度求得t的值;
(3)过Q作QE⊥x轴于E,在Rt△AQE中,可用t表示出AQ的长,进而根据∠OAB的度数表示出QE、AE的长,由S△PQR=S△OAB-S△OPR-S△APQ-S△BRQ即可求得S、t的函数关系式;根据所得函数的性质及自变量的取值范围即可求出S的最小值及对应的t的值;
(4)由于△APQ的腰和底不确定,需分类讨论:
①AP=AQ,可分别用t表示出两条线段的长,然后根据它们的等量关系求出此时t的值;
②PQ=AQ,过点Q作QD⊥x轴于D,根据等腰三角形三线合一的性质知:PA=2AD;可分别用t表示出PA、AD的长,然后根据它们的等量关系列方程求解;
③AP=PQ,过点Q做QH⊥AQ于H,方法同②.
解答  解:(1)在Rt△AOB中:∵OB=12cm,∠0AB=30°,
解:(1)在Rt△AOB中:∵OB=12cm,∠0AB=30°,
∴AB=2×12=24(cm),
∴AO=12$\sqrt{3}$cm;
(2)如图1,连接O′P,O′M.
当PM与⊙O′相切时,有:
∠PMO′=∠POO′=90°,
在Rt△PMO′和Rt△POO′中
∵$\left\{\begin{array}{l}{PO′=PO′}\\{OO′=O′M}\end{array}\right.$
∴Rt△PMO′≌Rt△POO′(HL).
∵∠0AB=30°,
∴∠OBA=60°,
∵O′M=O′B,
∴△O′BM是等边三角形,
∴∠BO′M=60°.
可得∠OO′P=∠MO′P=60°.
∴OP=OO′•tan∠OO′P
=6×tan60°=6$\sqrt{3}$.
又∵OP=2$\sqrt{3}$t,
∴2$\sqrt{3}$t=6$\sqrt{3}$,
解得:t=3.
即:t=3时,PM与⊙O′相切.
(3)如图1,过点Q作QE⊥x于点E.
∵∠BAO=30°,AQ=4t,
∴QE=$\frac{1}{2}$AQ=2t,
AE=AQ•cos∠OAB=4t×$\frac{\sqrt{3}}{2}$.
∴OE=OA-AE=12$\sqrt{3}$-2$\sqrt{3}$t.
∴Q点的坐标为(12$\sqrt{3}$-2$\sqrt{3}$t,2t),
S△PQR=S△OAB-S△OPR-S△APQ-S△BRQ
=$\frac{1}{2}$×12×12$\sqrt{3}$-$\frac{1}{2}$×2$\sqrt{3}$t×(12-2t)-$\frac{1}{2}$(12$\sqrt{3}$-2$\sqrt{3}$t)×2t-$\frac{1}{2}$×2t×(12$\sqrt{3}$-2$\sqrt{3}$t)
=6$\sqrt{3}$t2-36$\sqrt{3}$t+72$\sqrt{3}$
=6$\sqrt{3}$(t-3)2+18$\sqrt{3}$. (0<t<6)
当t=3时,S△PQR最小=18$\sqrt{3}$;
(4)分三种情况:如图2,
①当AP=AQ1=4t时,
∵OP+AP=12$\sqrt{3}$,
∴2$\sqrt{3}$t+4t=12$\sqrt{3}$.
解得:t=12$\sqrt{3}$-18;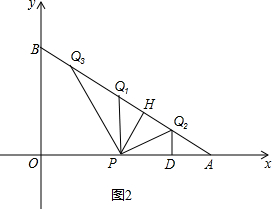
②当PQ2=AQ2=4t时,
过Q2点作Q2E⊥x轴于点E.
∴PA=2AE=2AQ2•cosA=4$\sqrt{3}$t,
即2$\sqrt{3}$t+4$\sqrt{3}$t=12$\sqrt{3}$,
解得:t=2;
③当PA=PQ3时,过点P作PH⊥AB于点H.
AH=PA•cos30°=(12$\sqrt{3}$-2$\sqrt{3}$t)•$\frac{\sqrt{3}}{2}$=18-3t,
AQ3=2AH=36-6t,
得36-6t=4t,
∴t=3.6.
综上所述,当t=2或t=3.6或t=12$\sqrt{3}$-18时,△APQ是等腰三角形.
点评 此题考查了切线的判定、全等三角形的判定和性质、二次函数的应用以及等腰三角形的判定和性质等知识,需注意的是(4)题在不确定等腰三角形腰和底的情况下,要充分考虑到各种可能的情况,以免漏解.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:填空题
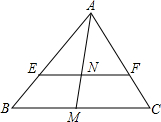 在△ABC中,EF∥BC,M是BC的中点,若△AEF的面积:梯形BCFE的面积=2:3,且AM=15,则AN=3$\sqrt{10}$.
在△ABC中,EF∥BC,M是BC的中点,若△AEF的面积:梯形BCFE的面积=2:3,且AM=15,则AN=3$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
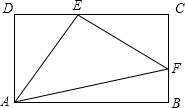 如图,四边形ABCD为矩形,E为CD上一点(不与C、D重合),F为BC上一点(不与C、B重合),△AEF的面积能否达到矩形ABCD面积的一半?请说明理由.
如图,四边形ABCD为矩形,E为CD上一点(不与C、D重合),F为BC上一点(不与C、B重合),△AEF的面积能否达到矩形ABCD面积的一半?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
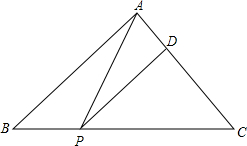 如图,在△ABC中,已知BC=4cm,AC=2$\sqrt{3}$cm,∠C=60°,在BC边上有一动点P,过P作PD∥AB,交AC于点D,试问:PB为多少时,△APD的面积最大?最大面积是多少?
如图,在△ABC中,已知BC=4cm,AC=2$\sqrt{3}$cm,∠C=60°,在BC边上有一动点P,过P作PD∥AB,交AC于点D,试问:PB为多少时,△APD的面积最大?最大面积是多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 截面可能是圆和三角形两类 | B. | 截面可能是圆和四边形两类 | ||
| C. | 截面可能是圆和五边形两类 | D. | 截面可能是三角形和四边形两类 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
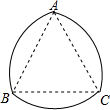 如图所示的图形叫弧三角形,又叫莱洛三角形,是机械学家莱洛首先进行研究的,弧三角形是这样画的:先画正三角形ABC,然后分别以点A,B,C为圆心,AB长为半径画弧,若正三角形ABC的边长为2cm,求弧三角形的周长.
如图所示的图形叫弧三角形,又叫莱洛三角形,是机械学家莱洛首先进行研究的,弧三角形是这样画的:先画正三角形ABC,然后分别以点A,B,C为圆心,AB长为半径画弧,若正三角形ABC的边长为2cm,求弧三角形的周长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com