
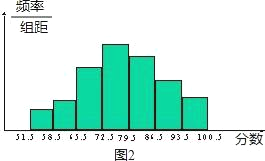
【题目】在一次环保知识测试中,三年一班的两名同学根据班级成绩(分数为整数)分别绘制了不同的频率分布直方图,如图1、2,已知图1从左到右每个小组的频率分别为0.04、0.08、0.24、0.32、0.20、0.12,其中68.5~76.5小组的频数为12;图2从左到右每个小组的频数之比为1:2:4:7:6:3:2,请结合条件和频率分布直方图回答下列问题:
(1)三年一班参加测试的人数是多少?
(2)若这次测试的成绩80分以上(含80分)为优秀,则优秀率是多少?
(3)若这次测试的成绩60分以上(含60分)为及格,则及格率是多少?

【答案】(1)50人(2)44%(3)96%
【解析】试题分析:(1)根据频率分布直方图知道68.5~76.5小组为第三小组,频率为0.24,频数为12,由此即可求出三年一班参加测试的人数;
(2)根据图2从左到右每个小组的频数之比为1:2:4:7:6:3:2可以求出各个小组的频率,然后就可以找到这次测试的成绩80分以上(含80分)的人数,也就可以求出优秀率;
(3)根据图1可以得到这次测试的成绩60分以上(含60分)的人数,然后除以总人数即可求出及格率是多少.
试题解析: (1)依题意得68.576.5小组为第三小组,频率为0.24,频数为12,
∴三年一班参加测试的人数是: ![]() 人.
人.
(2)由图2知,优秀人数从第五小组开始出现,
而图2从左到右每个小组的频数之比为1:2:4:7:6:3:2,
∴优秀率为![]()
(3)∵图1从左到右每个小组的频率分别为0.04、0.08、0.24、0.32、0.20、0.12,
∴这次测试成绩的及格率为![]()


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距离O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,
(1)A处是否会受到火车的影响,并写出理由
(2)如果A处受噪音影响,求影响的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,双曲线y=![]() 与直线y=﹣2x+2交于点A(﹣1,a).
与直线y=﹣2x+2交于点A(﹣1,a).
(1)求a,m的值;
(2)求该双曲线与直线y=﹣2x+2另一个交点B的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图1,在四边形ABCD中,点E、F分别是AB、CD的中点.过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连结GA、GB、GC、GD、EF,若∠AGD=∠BGC.

(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】机动车出发前油箱内有42升油,行驶若干小时后,途中在加油站加油若干升.油箱中余油量![]() (升)与行驶时间
(升)与行驶时间![]() (小时)之间的关系如图所示,根据下图回答问题:
(小时)之间的关系如图所示,根据下图回答问题:

(1)机动车行驶几小时后加油?加了多少油?
(2)试求加油前油箱余油量![]() 与行驶时间
与行驶时间![]() 之间的关系式;
之间的关系式;
(3)如果加油站离目的地还有350千米,车速为60千米/小时,照这样行驶,要到达目的地,油箱中的油是否够用?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,两半径为r的等圆⊙O1和⊙O2相交于M,N两点,且⊙O2过点O1.过M点作直线AB垂直于MN,分别交⊙O1和⊙O2于A,B两点,连接NA,NB.
(1)猜想点O2与⊙O1有什么位置关系,并给出证明;
(2)猜想△NAB的形状,并给出证明;
(3)如图2,若过M的点所在的直线AB不垂直于MN,且点A,B在点M的两侧,那么(2)中的结论是否成立,若成立请给出证明.
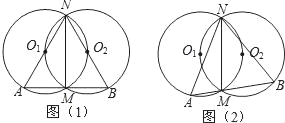
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=![]() x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,顶点为P.
x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,顶点为P.
(1)求这个二次函数的解析式,并在下面的坐标系中画出该二次函数的图象;
(2)设D为线段OC上的一点,满足∠DPC=∠BAC,求点D的坐标;
(3)在x轴上是否存在一点M,使以M为圆心的圆与AC、PC所在的直线及y轴都相切?如果存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一节快到了,甲、乙两家旅行社为了吸引更多的顾客,分别提出了赴某地旅游的团体优惠方法,甲旅行社的优惠方法是:买4张全票,其余人按半价优惠;乙旅行社的优惠方法是:一律按7折优惠,已知两家旅行社的原价均为每人100元。(旅游人数超过4人)
(1)分别表示出甲旅行社收费y1 ,乙旅行社收费y2与旅游人数x的函数关系式.
(2)就参加旅游的人数讨论哪家旅行社的收费更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
1637年笛卡尔在其《几何学》中,首次应用“待定系数法”将四次方程分解为两个二次方程求解,并最早给出因式分解定理.
他认为:对于一个高于二次的关于x的多项式,“![]() 是该多项式值为0时的一个解”与“这个多项式一定可以分解为(
是该多项式值为0时的一个解”与“这个多项式一定可以分解为(![]() )与另一个整式的乘积”可互相推导成立.
)与另一个整式的乘积”可互相推导成立.
例如:分解因式![]() .
.
∵![]() 是
是![]() 的一个解,∴
的一个解,∴![]() 可以分解为
可以分解为![]() 与另一个整式的乘积.
与另一个整式的乘积.
设![]()
而![]() ,则有
,则有
 ,得
,得![]() ,从而
,从而![]()
运用材料提供的方法,解答以下问题:
(1)①运用上述方法分解因式![]() 时,猜想出
时,猜想出![]() 的一个解为_______(只填写一个即可),则
的一个解为_______(只填写一个即可),则![]() 可以分解为_______与另一个整式的乘积;
可以分解为_______与另一个整式的乘积;
②分解因式![]() ;
;
(2)若![]() 与
与![]() 都是多项式
都是多项式![]() 的因式,求
的因式,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com