练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】规定：sin（﹣x）=﹣sinx，cos（﹣x）=cosx，sin（x+y）=sinxcosy+cosxsiny．

    据此判断下列等式成立的是 （写出所有正确的序号）

    ①cos（﹣60°）=﹣；

    ②sin75°=；

    ③sin2x=2sinxcosx；

    ④sin（x﹣y）=sinxcosy﹣cosxsiny．

    【答案】②③④．

    【解析】

    根据题意，得，①cos(－60°)＝cos60°= ≠ ，故错误；

    ②sin75°=sin（45°+30°)=sin45°×cos30°+cos45°×sin30°= ＝，故正确；

    ③sin2x＝sinx﹒cosx+cosx·sinx=2sinx·cosx，故正确；

    ④sin(x－y)＝sinx·cos（-y）+cosx·sin(-y)=sinx·cosy-cosx·siny，故正确，

    故答案为：②③④.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O的半径为5cm，弦AB为8cm，P为弦AB上的一动点，若OP的长度为整数，则满足条件的点P有____个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

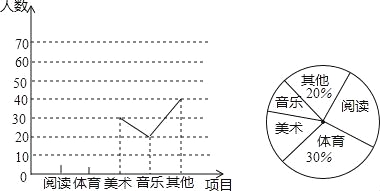
    【题目】某学校为了解该校学生的课余活动情况，抽样调查了部分同学，将所得数据处理后，制成折线统计图（部分）和扇形统计图（部分）如下：

    （1）在这次研究中，一共调查了 名学生．

    （2）补全频数分布折线图；

    （3）该校共有2200名学生，估计该校学生中爱好阅读的人数大约是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，I是ABC的内心，AI向延长线和△ABC的外接圆相交于点D，连接BI，BD，DC下列说法中错误的一项是（ ）

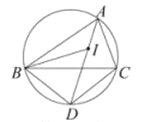
    A．线段DB绕点D顺时针旋转一定能与线段DC重合

    B．线段DB绕点D顺时针旋转一定能与线段DI熏合

    C．∠CAD绕点A顺时针旋转一定能与∠DAB重合

    D．线段ID绕点I顺时针旋转一定能与线段IB重合

    查看答案和解析>>

    科目：初中数学 来源： 题型：

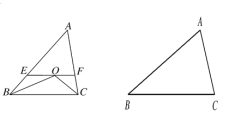
    【题目】如图，在△ABC中，∠ABC与∠ACB的平分线交于点O，过O做EF∥BC分别交AB、AC于E、F.

    （1）求证：EF=BE+CF.

    （2）在△ABC中，∠ABC的角平分线与∠ACB相邻的外角的平分线相交于点O，过O做EF∥BC分别交AB、AC于E、F，请你画出图形（不要求尺规作图），并直接写出EF、BE、CF之间的关系.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

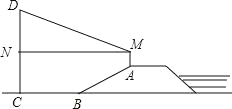
    【题目】如图，防洪大堤的横断面是梯形，背水坡AB的坡比i=1：，且AB=30m，李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°，己知地面BC宽30m，求高压电线杆CD的高度（结果保留三个有效数字，≈1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

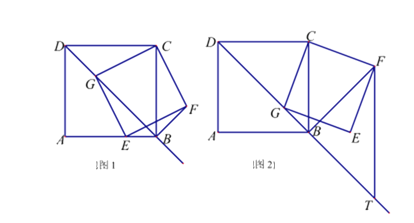
    【题目】我们知道：在小学已经学过“正方形的四条边都相等，正方形的四个内角都是直角”，试利用上述知识，并结合已学过的知识解答下列问题：

    如图1，在正方形ABCD中，G是射线DB上的一个动点（点G不与点D重合），以CG为边向下作正方形CGEF.

    （1）当点G在线段BD上时，求证：；

    （2）连接BF，试探索：BF，BG与AB的数量关系，并说明理由；

    （3）若AB=a（a是常数），如图2，过点F作FT∥BC，交射线DB于点T，问在点G的运动过程中，GT的长度是否会随着G点的移动而变化？若不变，请求出GT的长度；若变化，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点P在一次函数y=kx+b（k，b为常数，且k＜0，b＞0）的图象上，将点P向左平移1个单位，再向上平移2个单位得到点Q，点Q也在该函数y=kx+b的图象上．

    （1）k的值是 ；

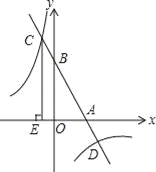
    （2）如图，该一次函数的图象分别与x轴、y轴交于A，B两点，且与反比例函数y=图象交于C，D两点（点C在第二象限内），过点C作CE⊥x轴于点E，记S1为四边形CEOB的面积，S2为△OAB的面积，若=，则b的值是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

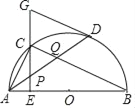
    【题目】如图，AB是半圆O的直径，点D是半圆O上一点，点C是 的中点，CE⊥AB于点E，过点D的切线交EC的延长线于点G，连接AD，分别交CE、CB于点P、Q，连接AC．

    （1）求证：GP＝GD；

    （2）求证：P是线段AQ的中点；

    （3）连接CD，若CD＝2，BC＝4，求⊙O的半径和CE的长．

    查看答案和解析>>

    同步练习册答案