
| ӡ��x��ǧ�ᣩ | 1��x��5 | x��5 |
| ��ɫ��Ԫ/�ţ� | 2.2 | 2.0 |
| �ڰף�Ԫ/�ţ� | 0.7 | 0.6 |
���� ��1���ư�Ѹ��ݲ�ҳ300Ԫ/�ţ��ڰ�ҳ50Ԫ/�ż��㼴�ɣ�1ǧ����ϵ�һ����Χ������ӡˢ��=����ɫ���ۡ�4+�ڰ��ۡ�6����1000��
��2���ٸ����踶��=�ư��+ӡˢ��=1500+����ɫ���ۡ�4+�ڰ��ۡ�6����1000x�����ɽ��
���п����ڵ�һ����Χ��Ҳ�п����ڵڶ�����Χ������ͬ�������̽�֣�
��� �⣺��1��ӡ��������������ư��Ϊ��4��300+6��50=1500��Ԫ����
ӡ��1ǧ�������ӡˢ�ѣ� 2.2��4+0.7��6����1000=13000��Ԫ����
�ʴ�Ϊ��1500��13000��
��2����������ã�y=1500+1000x•��2.2��4+0.7��6��
��y=13000x+1500��
�ڵ�1��x��5ʱ��13000x+1500��60 080
��x��4.5��
��x��5ʱ����ʱy=1500+1000x•��2.0��4+0.6��6��=11600x+1500��
��11600x+1500��60 080ʱ��
��x��5.05��
�������ӡ5.05ǧ�ᣮ
���� ���⿼����һ�κ�����Ӧ�ã��������Ĺؼ��Ƕ������⣬�ҵ��������ĵ�����ϵ����������IJ��ȹ�ϵʽ��


 �����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д� Сѧ�����ҵ���ϴ�ѧ������ϵ�д�
Сѧ�����ҵ���ϴ�ѧ������ϵ�д� ���Ž�����ٰθ��νӹ㶫���������ϵ�д�
���Ž�����ٰθ��νӹ㶫���������ϵ�д� �����������ҵ�������������ϵ�д�
�����������ҵ�������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��һ����ͼ�������ͨ���Ŀ���OB�ij���Ϊ1��������������OA����A1��A2��A3��������O�㵽A1��Ļ�����Ϊ��1Ȧ����Ϊ7������A1�㵽A2��Ļ�����Ϊ��2Ȧ����A2�㵽A3��Ļ�����Ϊ��3Ȧ�������������ƣ����10Ȧ�ij�Ϊ79��
��ͼ��һ����ͼ�������ͨ���Ŀ���OB�ij���Ϊ1��������������OA����A1��A2��A3��������O�㵽A1��Ļ�����Ϊ��1Ȧ����Ϊ7������A1�㵽A2��Ļ�����Ϊ��2Ȧ����A2�㵽A3��Ļ�����Ϊ��3Ȧ�������������ƣ����10Ȧ�ij�Ϊ79���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����O������AM�����ڵ�B����O�İ뾶Ϊ3������DA����OC��OA ����O�ڵ�C������BC����DA�ڵ�D��
��ͼ����O������AM�����ڵ�B����O�İ뾶Ϊ3������DA����OC��OA ����O�ڵ�C������BC����DA�ڵ�D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
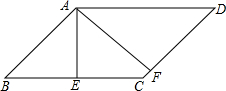 ��ͼ����ƽ���ı���ABCD�У�AE��BC��E��AF��CD��F����EAF=45�㣬��AE+AF=2$\sqrt{2}$����ƽ���ı���ABCD���ܳ��ǣ�������
��ͼ����ƽ���ı���ABCD�У�AE��BC��E��AF��CD��F����EAF=45�㣬��AE+AF=2$\sqrt{2}$����ƽ���ı���ABCD���ܳ��ǣ�������| A�� | 2 | B�� | 4$\sqrt{2}$ | C�� | 4 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com