
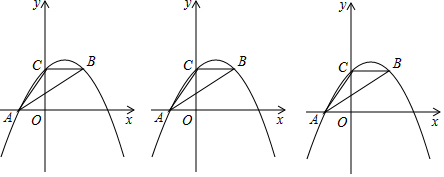
分析 (1)先计算出AC=5,再证明CB=CA=5,则B(5,4),然后利用待定系数法求抛物线解析式;
(2)先利用待定系数法确定直线AB的解析式为y=$\frac{1}{2}$x+$\frac{3}{2}$,设P(x,$\frac{1}{2}$x+$\frac{3}{2}$),则Q(x,-$\frac{1}{6}$x2+$\frac{5}{6}$x+4),所以PQ=-$\frac{1}{6}$x2+$\frac{5}{6}$x+4-($\frac{1}{2}$x+$\frac{3}{2}$)=-$\frac{1}{6}$x2+$\frac{1}{3}$x+$\frac{5}{2}$,然后利用二次函数的性质解决问题;
(3)作DH⊥PQ于H,PQ交x轴于E,如图,先计算出PA=2$\sqrt{5}$,再根据旋转的性质得∠APD=90°,PD=PA=2$\sqrt{5}$,接着通过△PDH≌△APE得到DH=PE=2,PH=AE=4,则D(-1,6),于是可利用待定系数法求出直线BD的解析式为y=-$\frac{1}{3}$x+$\frac{17}{3}$,则可确定M(1,$\frac{16}{3}$),再计算出BD=2$\sqrt{10}$,BM=$\frac{4\sqrt{10}}{3}$,然后证明△BMN∽△BDP,利用相似比计算MN的长.
解答 解:(1)∵A(-3,0)、C(0,4),
∴OA=3,OC=4,
∴AC=5,
∵AB平分∠CAO,
∴∠BAC=∠BAO,
∵BC∥x轴,
∴∠CBA=∠BAO,
∴∠BAC=∠CBA,
∴CB=CA=5,
∴B(5,4),
把A(-3,0)、C(0,4),B(5,4)代入y=ax2+bx+c得
$\left\{\begin{array}{l}{9a-3b+c=0}\\{c=4}\\{25a+5b+c=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{1}{6}}\\{b=\frac{5}{6}}\\{c=4}\end{array}\right.$,
∴抛物线解析式为y=-$\frac{1}{6}$x2+$\frac{5}{6}$x+4;
(2)设AB的解析式为y=px+q,
把A(-3,0),B(5,4)代入得$\left\{\begin{array}{l}{-3p+q=0}\\{5p+q=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{p=\frac{1}{2}}\\{q=\frac{3}{2}}\end{array}\right.$,
∴直线AB的解析式为y=$\frac{1}{2}$x+$\frac{3}{2}$,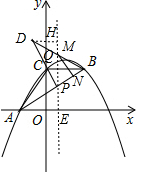
设P(x,$\frac{1}{2}$x+$\frac{3}{2}$),则Q(x,-$\frac{1}{6}$x2+$\frac{5}{6}$x+4),
∴PQ=-$\frac{1}{6}$x2+$\frac{5}{6}$x+4-($\frac{1}{2}$x+$\frac{3}{2}$)=-$\frac{1}{6}$x2+$\frac{1}{3}$x+$\frac{5}{2}$=-$\frac{1}{6}$(x-1)2+$\frac{8}{3}$,
∴当x=1时,PQ的值最大,
此时P点坐标为(1,2);
(3)作DH⊥PQ于H,PQ交x轴于E,如图,
PA=$\sqrt{(1+3)^{2}+{2}^{2}}$=2$\sqrt{5}$,
∵线段PA绕点P顺时针旋转90°,得线段PD,
∴∠APD=90°,PD=PA=2$\sqrt{5}$,
易得△PDH≌△APE,
∴DH=PE=2,PH=AE=4,
∴D(-1,6),
直线BD的解析式为y=-$\frac{1}{3}$x+$\frac{17}{3}$,
当x=1时,y=-$\frac{1}{3}$x+$\frac{17}{3}$=$\frac{16}{3}$,则M(1,$\frac{16}{3}$),
BD=$\sqrt{(5+1)^{2}+(4-6)^{2}}$=2$\sqrt{10}$,BM=$\sqrt{(5-1)^{2}+(4-\frac{16}{3})^{2}}$=$\frac{4\sqrt{10}}{3}$,
∵MN∥PD,
∴△BMN∽△BDP,
∴$\frac{MN}{DP}$=$\frac{BM}{BD}$,即$\frac{MN}{2\sqrt{5}}$=$\frac{\frac{4\sqrt{10}}{3}}{2\sqrt{10}}$,
∴MN=$\frac{4\sqrt{5}}{3}$.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和旋转的性质;会利用待定系数法求函数解析式;会利用两点间的距离公式和相似比计算线段的长;理解坐标与图形性质.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 请仅用无刻度的直尺,作出下列各图中∠AOB的平分线,保留作图痕迹.
请仅用无刻度的直尺,作出下列各图中∠AOB的平分线,保留作图痕迹.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
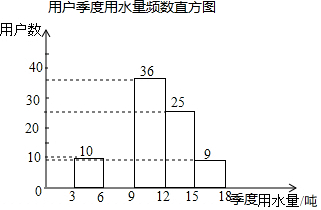 某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表:
某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表:| 平均用水量(吨) | 频数 | 频率 |
| 3<x≤6 | 10 | 0.1 |
| 6<x≤9 | m | 0.2 |
| 9<x≤12 | 36 | 0.36 |
| 12<x≤15 | 25 | n |
| 15<x≤18 | 9 | 0.09 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
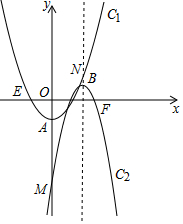 如图,抛物线C1:y1=tx2-1(t>0)和抛物线C2:y2=-4(x-h)2+1(h≥1).
如图,抛物线C1:y1=tx2-1(t>0)和抛物线C2:y2=-4(x-h)2+1(h≥1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com