练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”（如图），此图揭示了（a+b）n（n为非负整数）展开式的项数及各项系数的有关规律．
    例如：（a+b）0=1，它只有一项，系数为1；
    （a+b）1=a+b，它有两项，系数分别为1，1，系数和为2；
    （a+b）2=a2+2ab+b2，它有三项，系数分别为1，2，1，系数和为4；
    （a+b）3=a3+3a2b+3ab2+b3，它有四项，系数分别为1，3，3，1，系数和为8；
    …
    根据以上规律，解答下列问题：
    （1）（a+b）4展开式共有5项，系数分别为1，4，6，4，1；
    （2）写出（a+b）5的展开式：（a+b）5=a5+5a4b+10a3b2+10a2b3+5ab4+b5；
    （3）（a+b）n展开式共有（n+1）项，系数和为2n．

    分析 （1）本题通过阅读理解寻找规律，观察可得（a+b）n（n为非负整数）展开式的各项系数的规律：首尾两项系数都是1，中间各项系数等于（a+b）n-1相邻两项的系数和．因此可得（a+b）4的各项系数分别为1、（1+3）、（3+3）、（3+1）、1即可；
    （2）由（1）得出的规律，即可得出结果；
    （3）根据题意得出（a+b）n展开式共有（n+1）项，当a=b=1时，（a+b）n=2n即可．

    解答 解：（1）根据题意知，（a+b）4的展开后，共有5项，
    各项系数分别为1、（1+3）、（3+3）、（3+1）、1，
    即：1、4、6、4、1；
    故答案为：5，1，4，6，4，1；

    （2）根据题意得：（a+b）5的展开式为a5+5a4b+10a3b2+10a2b3+5ab4+b5．
    故答案为a5+5a4b+10a3b2+10a2b3+5ab4+b5；

    （3）当a=b=1时，（a+b）n=2n．
    故答案为：（n+1），2n．

    点评 本题考查了完全平方公式、（a+b）n展开式；关键在于观察、分析已知数据，找出规律是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    12．已知m是方程2x2-x-1=0的一个根，则代数式6m2-3m的值等于（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．以下列哪组数为边，可以得到直角三角形的是（　　）
    A．9，16，25B．8，15，17C．6，8，14D．10，12，13

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

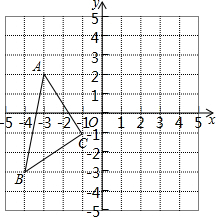    10．如图坐标系中，A（-3，2），B（-4，-3），C（-1，-1）．
    （1）在图中作出△ABC关于y轴对称的△A1B1C1；
    （2）写出点△A1，B1，C1的坐标（直接写答案）：
    A1（3，2）；
    B1（4，-3）；
    C1（1，-1）；
    （3）求出△A1B1C1的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下列说法中，正确的是（　　）
    A．$\sqrt{16}$=±4B．-22的平方根是±2
    C．64的立方根是±4D．-$\sqrt{5}$是5的一个平方根

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．若ab＞0，求$\frac{a}{|a|}$+$\frac{b}{|b|}$+$\frac{ab}{|ab|}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．若点（-5，y1），（-3，y2），（2，y3），都在y=-$\frac{6}{x}$的图象上，则把y1，y2，y3用“＜”按从小到大排
    列为：y3＜y1＜y2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．数学老师在课堂上提出一个问题：“通过探究知道：$\sqrt{2}$≈1.414…，它是个无限不循环小数，也叫无理数，它的整数部分是1，那么有谁能说出它的小数部分是多少”，小明举手回答：它的小数部分我们无法全部写出来，但可以用$\sqrt{2}$-1来表示它的小数部分，张老师夸奖小明真聪明，肯定了他的说法．现请你根据小明的说法解答：
    （1）$\sqrt{5}$的小数部分是a，$\sqrt{37}$的整数部分是b，求a+b-$\sqrt{5}$的值．
    （2）已知8+$\sqrt{3}$=x+y，其中x是一个整数，0＜y＜1，求3x+（y-$\sqrt{3}$）2015的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．已知：角α的终边经过点（$\frac{1}{2}$，-$\frac{\sqrt{2}}{2}$），则tanα=（　　）
    A．$\frac{1}{2}$B．-$\frac{\sqrt{6}}{3}$C．-$\frac{\sqrt{3}}{2}$D．-$\sqrt{2}$

    查看答案和解析>>

    同步练习册答案