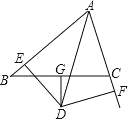
【题目】如图，已知∠A=∠C，AD⊥BE于点F，BC⊥BE，点E，D，C在同一条直线上.
(1)判断AB与CD的位置关系，并说明理由；
(2)若∠ABC=120°，求∠BEC的度数.
学练快车道快乐假期寒假作业系列答案
新思维寒假作业系列答案科目：初中数学 来源： 题型：
【题目】如图，G 为 BC 的中点，且 DG⊥BC，DE⊥AB 于 E，DF⊥AC 于 F， BE＝CF．
（1）求证：AD 是∠BAC 的平分线；
（2）如果 AB＝8，AC＝6，求 AE 的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
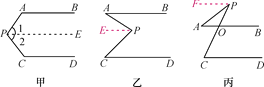
【题目】阅读下列解答过程：（1）如图甲，AB∥CD，探索∠P与∠A，∠C之间的关系．
（2）如图乙和图丙，AB∥CD，请根据上述方法分别探索两图中∠P与∠A，∠C之间的关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
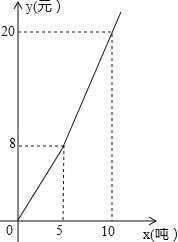
【题目】随着地球上的水资源日益枯竭，各级政府越来越重视节约用水．某市民生活用水按“阶梯水价”方式进行收费，人均月生活用水收费标准如图所示，图中 x 表示人均月生活用水的吨数，y 表示收取的人均月生活用水费（元）．请根据图象信息，回答下列问题：
(1)该市人均月生活用水的收费标准是：不超过 5 吨，每吨按 元收取； 超过 5 吨的部分，每吨按 元收取；
(2)当 x＞5 时，求 y 与 x 的函数关系式；
(3)若某个家庭有 5 人，五月份的生活用水费共 76 元，则该家庭这个月用了多少吨生活用水？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，⊙O的半径为 
，BD是⊙O的切线，D为切点，过圆上一点C作BD的垂线，垂足为B，BC=3，点A是优弧CD的中点，则sin∠A的值是（ ）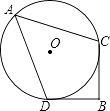 
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，⊙O中，FG、AC是直径，AB是弦，FG⊥AB，垂足为点P，过点C的直线交AB的延长线于点D，交GF的延长线于点E，已知AB=4，⊙O的半径为 
． 
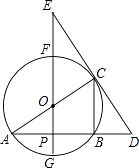
（1）分别求出线段AP、CB的长；
（2）如果OE=5，求证：DE是⊙O的切线；
（3）如果tan∠E= 
，求DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，为厉行节能减排，倡导绿色出行，某公司拟在我市甲、乙两个街道社区投放一批共享单车（俗称“小黄车”），这批自行车包括A、B两种不同款型．
成本单价 （单位：元） | 投放数量 （单位：辆） | 总价（单位：元） | |
A型 | x | 50 | 50x |
B型 | x+10 | 50 |
|
成本合计（单位：元） | 7500 | ||
问题1：看表填空
如图2所示，本次试点投放的A、B型“小黄车”共有 辆；用含有x的式子表示出B型自行车的成本总价为 ；
问题2：自行车单价
试求A、B两型自行车的单价各是多少？
问题3：投放数量
现在该公司采取如下方式投放A型“小黄车”：甲街区每100人投放n辆，乙街区每100人投放（n+2）辆，按照这种投放方式，甲街区共投放1500辆，乙街区共投放1200辆，如果两个街区共有
人，求甲街区每100人投放A型“小黄车”的数量．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了迎接“六一”国际儿童节，某童装品牌专卖店准备购进甲、乙两种童装，这两种童装的进价和售价如下表：
价格 | 甲 | 乙 |
进价（元/件） | m | m+20 |
售价（元/件） | 150 | 160 |
如果用5000元购进甲种童装的数量与用6000元购进乙种童装的数量相同．
（1）求m的值；
（2）要使购进的甲、乙两种童装共200件的总利润（利润＝售价﹣进价）不少于8980元，且甲种童装少于100件，问该专卖店有哪几种进货方案？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
