
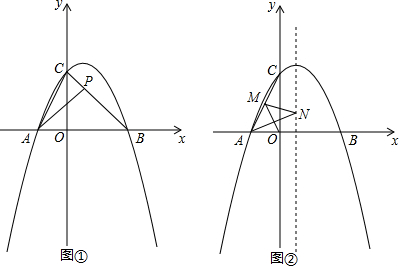
���� ��1�����ݴ���ϵ������ü��ɣ�
��2����A��AH��BC��H������S��ABP��S��APC=3��2���BP��CP=3��2����P��PP���x����P�䣬���BPP��ס�BCO���������������ζ�Ӧ�߳ɱ����������PP��=$\frac{3}{5}$CO=$\frac{6}{5}$���ó���PΪԲ�ģ���x�����е�Բ�İ뾶��
��3������O����AC�ĶԳƵ�O�䣬OO�佻AC��H����O����O��T��x����T����֤�á�O��TO�ס�AOC���ó�$\frac{O��T}{OA}$=$\frac{OO��}{AC}$=$\frac{OT}{OC}$�����ݹ��ɶ������AC��Ȼ����������������ʽ���OH���������OO�䣬Ȼ��������Һ������sin��O��OT=$\frac{O��T}{OO��}$=sin��ACO=$\frac{1}{\sqrt{5}}$���Ӷ����O��T=$\frac{4}{5}$��ͬ��OT=$\frac{8}{5}$���������O������꣬����O��M��BN������OM=O��M��AN=BN������OM+MN+AN=O��M+MN+BN����֪��O�䣬M��N��B��һ��ֱ����ʱOM+MN+ANȡ��Сֵ�����ݹ��ɶ������O��B=$\frac{2}{5}$$\sqrt{85}$����OM+MN+AN����Сֵ������O�䣨-$\frac{8}{5}$��$\frac{4}{5}$����B��2��0�������ֱ��O��B�Ľ���ʽΪ��y=-$\frac{2}{9}$x+$\frac{4}{9}$����A��-1��0����B��2��0������������ߵĶԳ���x=$\frac{1}{2}$����x=$\frac{1}{2}$����ֱ��O��B�Ľ���ʽ�������N�����꣮
��� 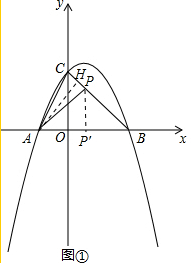 �⣺��1���������$\left\{\begin{array}{l}{a-b+c=0}\\{4a+2b+c=0}\\{c=2}\end{array}\right.$��
�⣺��1���������$\left\{\begin{array}{l}{a-b+c=0}\\{4a+2b+c=0}\\{c=2}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-1}\\{b=1}\\{c=2}\end{array}\right.$��
�������ߵĽ���ʽΪ��y=-x2+x+2��
��2����ͼ�٣���A��AH��BC��H��S��ABP=$\frac{1}{2}$BP•AH��S��APC=$\frac{1}{2}$CP•AH��
��S��ABP��S��APC=BP��CP=3��2��
��P��PP���x����P�䣬���BPP��ס�BCO��
��$\frac{PP��}{CO}$=$\frac{BP}{BC}$=$\frac{3}{5}$��
��PP��=$\frac{3}{5}$CO=$\frac{6}{5}$��
����PΪԲ�ĵ�Բ��x�����У�
���Բ�뾶=PP��=$\frac{6}{5}$��
��3����ͼ�ڣ�����֪A��B������ڶԳ���Գƣ�����O����AC�ĶԳƵ�O�䣬OO�佻AC��H����O����O��T��x����T��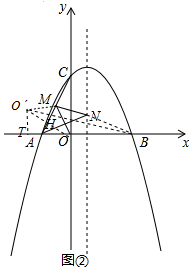 ��OO���AC��
��OO���AC��
���AOH���OAC����
�֡ߡ�C���OAC���࣬
���AOH=��C��
�ߡ�OTO��=��AOC=90�㣬
���O��TO�ס�AOC��
��$\frac{O��T}{OA}$=$\frac{OO��}{AC}$=$\frac{OT}{OC}$��
��C��0��2����A��-1��0����
��AC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$��
��S��AOC=$\frac{1}{2}$OA•OC=$\frac{1}{2}$AC•OH��
��OO��=2OH=2��$\frac{OA•OC}{AC}$=$\frac{4}{5}$$\sqrt{5}$��
��sin��O��OT=$\frac{O��T}{OO��}$=sin��ACO=$\frac{1}{\sqrt{5}}$��
��O��T=$\frac{4}{5}$��ͬ��OT=$\frac{8}{5}$��
��O�䣨-$\frac{8}{5}$��$\frac{4}{5}$����
����O��M��BN��
��OM=O��M��AN=BN��
��OM+MN+AN=O��M+MN+BN��
��֪��O�䣬M��N��B��һ��ֱ����ʱOM+MN+ANȡ��Сֵ��
O��B=$\sqrt{O��{T}^{2}+B{T}^{2}}$=$\frac{2}{5}$$\sqrt{85}$��
��O�䣨-$\frac{8}{5}$��$\frac{4}{5}$����B��2��0����
��ֱ��O��B�Ľ���ʽΪ��y=-$\frac{2}{9}$x+$\frac{4}{9}$��
��A��-1��0����B��2��0����
�������ߵĶԳ���x=$\frac{1}{2}$��
��x=$\frac{1}{2}$����ã�y=$\frac{1}{3}$
��N��$\frac{1}{2}$��$\frac{1}{3}$����
���� �����Ƕ��κ������ۺ��⣬�����˴���ϵ���������ʽ�����������Ƶ��ж������ʣ����ɶ�����Ӧ�ã����Һ����Լ����·�����⣬�������մ���ϵ���������������Ƶ��ж������������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3�� | B�� | 4�� | C�� | 5�� | D�� | 6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
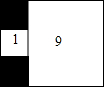 ��ͼ�������������������ε�����ֱ���1��9����ô��������Ӱ���ֵ������2��
��ͼ�������������������ε�����ֱ���1��9����ô��������Ӱ���ֵ������2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
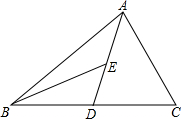 ��ͼ��ADΪ��ABC�����ߣ�BEΪ��ABD�����ߣ�
��ͼ��ADΪ��ABC�����ߣ�BEΪ��ABD�����ߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6�� | B�� | 9�� | C�� | 11�� | D�� | 12�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
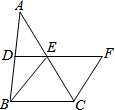 ��ͼ���ڡ�ABC�У�D��E�ֱ���AB��AC���е㣬BE=2DE���ӳ�DE��F��ʹ��EF=BE������CF��
��ͼ���ڡ�ABC�У�D��E�ֱ���AB��AC���е㣬BE=2DE���ӳ�DE��F��ʹ��EF=BE������CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 Ϊ�˴Ӽף�������ѧ����ѡ��һ�˲μӾ�����ѧУÿ���¶����ǵ�ѧϰ������һ�β��飬��ͼ��������ǰ5�β���ɼ�������ͳ��ͼ����ÿ�β��Եijɼ���Ϊ5�ı�����
Ϊ�˴Ӽף�������ѧ����ѡ��һ�˲μӾ�����ѧУÿ���¶����ǵ�ѧϰ������һ�β��飬��ͼ��������ǰ5�β���ɼ�������ͳ��ͼ����ÿ�β��Եijɼ���Ϊ5�ı������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com