
【题目】如图,菱形ABCD中,对角线AC,BD相交于点O,AC=12cm,BD=16cm,动点N从点D出发,沿线段DB以2cm/s的速度向点B运动,同时动点M从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随之停止,设运动时间为t(s)(t>0),以点M为圆心,MB长为半径的⊙M与射线BA,线段BD分别交于点E,F,连接EN. 
(1)求BF的长(用含有t的代数式表示),并求出t的取值范围;
(2)当t为何值时,线段EN与⊙M相切?
(3)若⊙M与线段EN只有一个公共点,求t的取值范围.
【答案】
(1)解:连接MF.
∵四边形ABCD是菱形,
∴AB=AD,AC⊥BD,OA=OC=6,OB=OD=8,
在Rt△AOB中,AB= ![]() =10,
=10,
∵MB=MF,AB=AD,
∴∠ABD=∠ADB=∠MFB,
∴MF∥AD,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BF= ![]() t(0<t≤8).
t(0<t≤8).
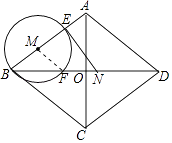
(2)解:当线段EN与⊙M相切时,易知△BEN∽△BOA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴t= ![]() .
.
∴t= ![]() s时,线段EN与⊙M相切.
s时,线段EN与⊙M相切.
(3)解:①由题意可知:当0<t≤ ![]() 时,⊙M与线段EN只有一个公共点.
时,⊙M与线段EN只有一个公共点.
②当F与N重合时,则有 ![]() t+2t=16,解得t=
t+2t=16,解得t= ![]() ,
,
关系图象可知, ![]() <t<8时,⊙M与线段EN只有一个公共点.
<t<8时,⊙M与线段EN只有一个公共点.
综上所述,当0<t≤ ![]() 或
或 ![]() <t<8时,⊙M与线段EN只有一个公共点.
<t<8时,⊙M与线段EN只有一个公共点.
【解析】(1)连接MF.只要证明MF∥AD,可得 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解方程即可;(2)当线段EN与⊙M相切时,易知△BEN∽△BOA,可得
,解方程即可;(2)当线段EN与⊙M相切时,易知△BEN∽△BOA,可得 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解方程即可;(3)①由题意可知:当0<t≤
,解方程即可;(3)①由题意可知:当0<t≤ ![]() 时,⊙M与线段EN只有一个公共点.②当F与N重合时,则有
时,⊙M与线段EN只有一个公共点.②当F与N重合时,则有 ![]() t+2t=16,解得t=
t+2t=16,解得t= ![]() ,观察图象即可解决问题;
,观察图象即可解决问题;


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于D,则旋转角等于( ) 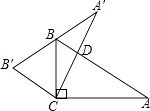
A.70°
B.80°
C.60°
D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明袋子中装有1个红球,2个黄球,这些球除颜色外都相同,小明搅匀后从中任意摸出一个球,记录颜色后放回、搅匀,再从中任意摸出1个球,用树状图或列表法列出摸出球的所有等可能情况,并求两次摸出的球都是黄色的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求△MCB的面积S△MCB .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】主题班会课上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点: 
A.放下自我,彼此尊重; B.放下利益,彼此平衡;
C.放下性格,彼此成就; D.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟,根据同学们的选择情况,小明绘制了下面两幅不完整的图表,请根据图表中提供的信息,解答下列问题:
观点 | 频数 | 频率 |
A | a | 0.2 |
B | 12 | 0.24 |
C | 8 | b |
D | 20 | 0.4 |
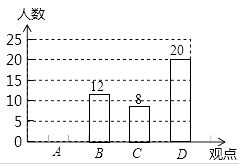
(1)参加本次讨论的学生共有人;
(2)表中a= , b=;
(3)将条形统计图补充完整;
(4)现准备从A,B,C,D四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点D(合理竞争,合作双赢)的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,取BC的中点P.当点B从点O向x轴正半轴移动到点M(2,0)时,则点P移动的路线长为 . 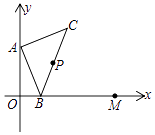
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等腰直角三角形,∠A=90°,D是腰AC上的一个动点,过C作CE垂直于BD的延长线,垂足为E,如图1
(1)求证:ADCD=BDDE;
(2)若BD是边AC的中线,如图2,求 ![]() 的值;
的值;
(3)如图3,连接AE.若AE=EC,求 ![]() 的值.
的值.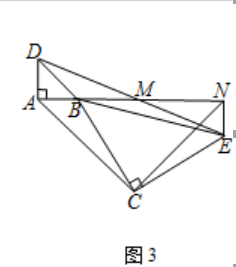
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣ ![]() x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
(1)求抛物线的解析式;
(2)在AC上方的抛物线上有一动点P.
①如图1,当点P运动到某位置时,以AP,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P的坐标;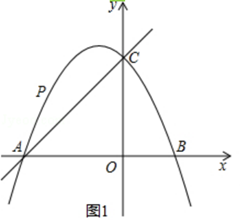
②如图2,过点O,P的直线y=kx交AC于点E,若PE:OE=3:8,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(列方程(组)及不等式解应用题)
春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com