
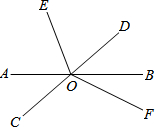
 如图,直线AB、CD相交于点0,OE平分∠AOD,∠FOC=96°,∠BOF=40°,试求∠AOE的度数.
如图,直线AB、CD相交于点0,OE平分∠AOD,∠FOC=96°,∠BOF=40°,试求∠AOE的度数. 分析 先求出∠BOC的度数,根据对顶角相等,得到∠AOD=∠BOC=136°,再利用OE平分∠AOD,所以∠AOE=$\frac{1}{2}∠AOD$=$\frac{1}{2}×13{6}^{°}$=68°.
解答 解:∵∠FOC=96°,∠BOF=40°,
∴∠BOC=∠FOC+∠BOF=96°+40°=136°,
∵∠AOD与∠BOC是对顶角,
∴∠AOD=∠BOC=136°,
∵OE平分∠AOD,
∴∠AOE=$\frac{1}{2}∠AOD$=$\frac{1}{2}×13{6}^{°}$=68°.
点评 本题考查对顶角和角平分线,解决本题的关键是根据对顶角相等得到∠AOD=∠BOC.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:解答题
| 月用水量(吨) | 单价(元/吨) |
| 不大于10吨部分 | 1.5 |
| 大于10吨不大于m吨部分(20≤m≤50) | 2 |
| 大于m吨部分 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
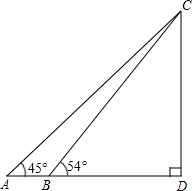 某校数学兴趣小组要测量天塔CD的高度,如图,他们在点A处测得天塔最高点C的仰角为45°,再往天塔方向前进至点B处测得最高点C的仰角为54°,AB=27m,根据这个兴趣小组测得的数据,计算天塔的高度CD(tan36°≈0.73,结果保留整数).
某校数学兴趣小组要测量天塔CD的高度,如图,他们在点A处测得天塔最高点C的仰角为45°,再往天塔方向前进至点B处测得最高点C的仰角为54°,AB=27m,根据这个兴趣小组测得的数据,计算天塔的高度CD(tan36°≈0.73,结果保留整数).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com