
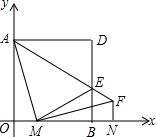
 在图中,正方形AOBD的边AO,BO在坐标轴上,若它的面积为16,点M从O点以每秒1个单位长度的速度沿x轴正方向运动,当M到达B点时,运动停止.连接AM,过M作AM⊥MF,且满足AM=MF,连接AF交BD于E点,过F作FN⊥x轴于N,连接ME.设点M运动时间为t(s).
在图中,正方形AOBD的边AO,BO在坐标轴上,若它的面积为16,点M从O点以每秒1个单位长度的速度沿x轴正方向运动,当M到达B点时,运动停止.连接AM,过M作AM⊥MF,且满足AM=MF,连接AF交BD于E点,过F作FN⊥x轴于N,连接ME.设点M运动时间为t(s).分析 (1)由正方形的面积可求得正方形的边长,从而可得到点D的坐标,由题意可知OM=t,且M在x轴上,故此可得到点M的坐标;
(2)先依据AAS证明△AMO≌△MFN,从而得到OM=FN,OA=MN,接下来由三角形的面积公式可求得OM的长,从而得到t得值;
(3)可分为AM=EM、AE=ME、AM=AE三种情况.其中AM=EM的情况不成立;当AE=ME时,可依据AAS证明△MEB≌△EAD,从而得到BE=AD,于是可得到M与点B重合从而求得t的值;当AM=AE时,可证明MO=MH=HE=DE,从而可求得ME=2t,MB=4-t,然后在△MBE中依据勾股定理列出关于t的方程,从而可取得t的值.
解答 解:(1)∵正方形AOBD的面积为为16,
∴正方形的边长为4,即OB=BD=4.
∴D(4,4).
∵OM=t,点M在x轴上,
∴M(t,0).
(2)∵AM⊥MF,
∴∠AMF=90°.
∴∠AMO+∠FMN=90°.
又∵∠OAM+∠AMO=90°,
∴∠OAM=∠FMN.
在△AMO于△MFN中,$\left\{\begin{array}{l}{∠MOA=∠FNM}\\{∠MAO=∠FMN}\\{AM=MF}\end{array}\right.$,
∴△AMO≌△MFN(AAS).
∴OM=FN,OA=MN.
∴$\frac{1}{2}$AO•OM=$\frac{1}{2}$MN•FN=$\frac{8}{3}$,$\frac{1}{2}$×4×t=$\frac{8}{3}$,解得:t=$\frac{4}{3}$.
(3)①∵△AMF为等腰直角三角形,
∴MF=AM≠ME.
∴AM=EM这种情况不成立.
②当AE=ME时.
∵△AMF为等腰直角三角形,
∴∠MAE=45°.
∵AE=ME,
∴∠MAE=∠AME=45°.
∴∠AEM=90°.
∴∠AED+∠MEB=90°.
又∵∠AED+∠EAD=90°,
∴∠MEB=∠EAD.
在△MEB和△EDA中$\left\{\begin{array}{l}{∠MEB=∠EAD}\\{∠MBE=∠D}\\{ME=AE}\end{array}\right.$,
∴△MEB≌△EAD(AAS).
∴BE=AD.
∴点B与点D重合,点M与点B重合.
∴t=4.
③当AM=AE时,如图所示:连接AB交ME于点H.
∵在Rt△AOM和Rt△ADE中,$\left\{\begin{array}{l}{AM=AE}\\{AO=AD}\end{array}\right.$,
∴Rt△AOM≌△Rt△ADE.
∴DE=OM=t,∠MAO=∠DAE=22.5°.
∵四边形AOBD为正方形,
∴∠BAO=∠DAB=45°.
∴∠MAH=∠EAH=22.5°.
∴∠MAH=∠EAH=∠OAM=∠DAE=22.5°.
∴AH⊥ME.
∴MO=MH=t,HE=DE=t.
∴ME=MH+HE=2t.
∵MB=BE=4-t,由勾股定理得:ME2=MB2+BE2,即2(4-t)2=4t2.
解得:t=4$\sqrt{2}$-4,t=-4-4$\sqrt{2}$(舍去).
综上所述,当t=4或y=4$\sqrt{2}$-4时,△AME为等腰三角形.
点评 本题主要考查的是四边形的综合应用,解答本题主要应用了正方形的性质、全等三角形的性质和判定、勾股定理的应用,依据勾股定理列出关于t的方程是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | x≥-1 | B. | x≠2 | C. | x≥-1且x≠2 | D. | 以上都不正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
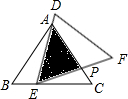 如图,在△ABC中,已知AB=AC=6,BC=8,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于P点.
如图,在△ABC中,已知AB=AC=6,BC=8,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于P点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com