
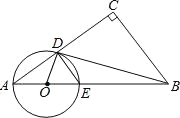
【题目】如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.
(1)判断直线BD与⊙O的位置关系,并证明你的结论;
(2)若AD:AO=8:5,BC=3,求BD的长.
【答案】(1)BD是⊙O的切线;理由参见解析;(2)![]() .
.
【解析】
试题分析:(1)由等腰三角形的性质和已知得出∠ODA=∠CBD,由直角三角形的性质得出∠CBD+∠CDB=90°,因此∠ODA+∠CDB=90°,得出∠ODB=90°,即可得出结论;(2)设AD=8k,则AO=5k,AE=2OA=10k,由圆周角定理得出∠ADE=90°,△ADE∽△BCD,得出对应边成比例![]() ,即可求出BD的长.
,即可求出BD的长.
试题解析:(1)BD是⊙O的切线;理由如下:∵OA=OD,∴∠ODA=∠A,∵∠CBD=∠A,∴∠ODA=∠CBD,∵∠C=90°,∴∠CBD+∠CDB=90°,∴∠ODA+∠CDB=90°,∴∠ODB=90°,即BD⊥OD,∴BD是⊙O的切线;(2)设AD=8k,则AO=5k,AE=2OA=10k,∵AE是⊙O的直径,∴∠ADE=90°,∴∠ADE=∠C,又∵∠CBD=∠A,∴△ADE∽△BCD,∴![]() ,即
,即![]() ,解得:BD=
,解得:BD=![]() .所以BD的长是
.所以BD的长是![]() .
.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】小华拿24元钱购买火腿肠和方便面,已知一盒方便面3元,一根火腿肠2元,他买了4盒方便面,x根火腿肠,则关于x的不等式表示正确的是( )
A.3×4+2x<24
B.3×4+2x≤24
C.3x+2×4≤24
D.3x+2×4≥24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个点的横、纵坐标均为整数,那么我们称这个点是格点,如图,A、B两点在函数y= ![]() (x>0)的图象上,则图中阴影部分(不包括边界)所含格点的个数为( )
(x>0)的图象上,则图中阴影部分(不包括边界)所含格点的个数为( ) 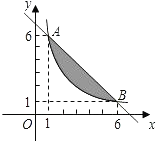
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD的边AB=3,BC=4,点P是BC边上一动点(不与B、C重合),现将△ABP沿AP翻折,得到△AFP,再在CD边上选择适当的点E,将△PCE沿PE翻折,得到△PME,且直线PF、PM重合,若点F落在矩形纸片的内部,则CE的最大值是 .
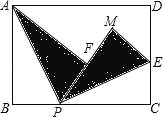
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com