
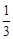 ,延长OE到点F,使EF=2OE.
,延长OE到点F,使EF=2OE.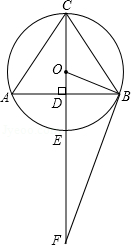
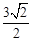 (2)证明见解析
(2)证明见解析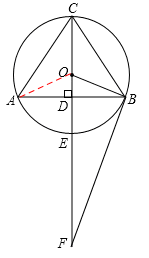
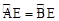 。
。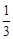 ,∴cos∠BOD=
,∴cos∠BOD=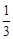 ,
,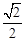 。
。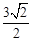 ,即⊙O的半径为
,即⊙O的半径为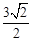 。
。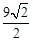 。∴
。∴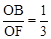 。
。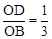 ,∴
,∴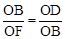 。
。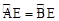 ,由已知利用圆周角定理可得到∠BOE=∠ACB,可得到cos∠BOD=cos∠ACB=
,由已知利用圆周角定理可得到∠BOE=∠ACB,可得到cos∠BOD=cos∠ACB=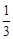 ,在Rt△BOD中,设OD=x,则OB=3x,利用勾股定理可计算出x=
,在Rt△BOD中,设OD=x,则OB=3x,利用勾股定理可计算出x=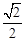 ,则OB=3x=
,则OB=3x=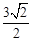 。
。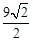 ,则
,则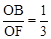 ,而
,而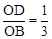 ,于是得到
,于是得到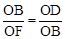 ,根据相似三角形的判定即可得到△OBF∽△ODB,根据相似三角形的性质有∠OBF=∠ODB=90°,然后根据切线的判定定理即可得到结论。
,根据相似三角形的判定即可得到△OBF∽△ODB,根据相似三角形的性质有∠OBF=∠ODB=90°,然后根据切线的判定定理即可得到结论。

 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源:不详 题型:填空题
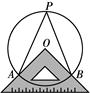
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
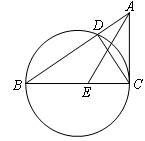
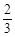 ,tan∠AEC=
,tan∠AEC=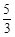 ,求圆的直径.
,求圆的直径.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
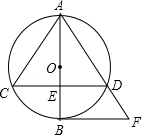
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
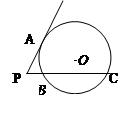
| A.4㎝ | B.16㎝ |
| C.20㎝ | D.2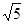 ㎝ ㎝ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com