
| 购票人数 | 1-30人 | 31-60人 | 60人以上 |
| 票价 | 无折扣 | 超出30人的部分,票价打八折 | 超出60人的部分,票价打五折 |
分析 设甲班有x人,乙班有y人,根据“①超出60人部分的费用=545-(300+30×10×0.8)、②乙班费用+甲班费用=598”列方程组求解可得.
解答 解:设甲班有x人,乙班有y人,
根据题意可得$\left\{\begin{array}{l}{(x+y-60)×5=545-540}\\{10y+300+(x-30)×8=598}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=36}\\{y=25}\end{array}\right.$,
即甲班有36人,乙班有25人,
故答案为:36,25.
点评 本题主要考查二元一次方程组的应用,弄清表格中分段收费标准,根据费用确定其中蕴含的相等关系:①超出60人部分的费用=545-(300+30×10×0.8)、②乙班费用+甲班费用=598是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,点C在射线OA上,CE平分∠ACD. OF平分∠COB并与射线CD交于点F。

(1)依题意补全图形;
(2)若∠COB+∠OCD=180°,求证:∠ACE=∠COF。
请将下面的证明过程补充完整。
证明:∵CE平分∠ACD,OF平分∠COB,
∴∠ACE=______________,∠COF= ∠COB。
∠COB。
(理由: _____________________________________)
∵点C在射线OA上,
∴∠ACD+∠OCD=180°。
∵∠COB+∠OCD=180°,
∴∠ACD=∠____________。
(理由: ___________________________________)
∴∠ACE=∠COF。
查看答案和解析>>
科目:初中数学 来源:2016-2017学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:单选题
甲、乙两人同时开始采摘樱桃,甲平均每小时采摘8公斤樱桃,乙平均每小时采摘7公斤樱桃。采摘同时结束后,甲从他采摘的樱桃中取出1公斤给了乙,这时两人的樱桃一样多。他们采摘樱桃用了多长时间?设他们采摘了x小时,则下面所列方程中正确的是( )
A. 8x-1=7x+1 B. 8x-1=7x C. 8x+l=7x D. 8x+l=7x-1
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间(秒) 路程(米) | 从比赛开始到 匀速跑前 | 从比赛开始到 匀速跑完100秒 | 从比赛开始到 匀速跑完200秒 |
| 小明 | 1600 | 1600+100a | 1600+200a |
| 小刚 | 1450 | 1450+100b | 1450+200b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
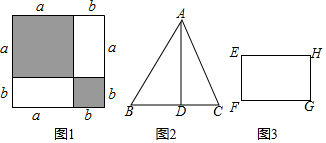
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com