
【题目】如图1,将一条两边互相平行的纸带折叠。
(1)若图中α=70,则β=°;
(2)探求图中α与β的数量关系;
(3)在图1的基础上继续折叠,使得图1中的CD边与CB边重合(如图2),若继续沿CB边折叠,CE边恰好平分∠ACB,直接写出此时β的大小。
【答案】
(1)55
(2)
解:因为纸带两边平行,
所以∠OAC=α,
由折叠可得∠BAP=β,
由平角的定义可得∠OAC+β+∠BAP=180°,
即α+2β=180°,
则β=90°- ![]() .
.
(3)
解:由折叠可得2∠BCE=∠BCD(图1中)=180°-α=2β,即∠BCE=β.
而∠BCE= ![]() ∠ACB,所以∠ACB=2β.
∠ACB,所以∠ACB=2β.
因为纸带两边平行,
所以∠ACB+β=180°,
则3β=180°,
解得β=60°.
【解析】(1)因为纸带两边平行,
所以∠OAC=α,
由折叠可得∠BAP=β,
由平角的定义可得∠OAC+β+∠BAP=180°,
即α+2β=180°,
则β=90°- ![]() =55°.
=55°.
所以答案是55.
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


科目:初中数学 来源: 题型:
【题目】中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是用八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为S1 , S2 , S3 , 若S1+S2+S3=18,则正方形EFGH的面积为( ) 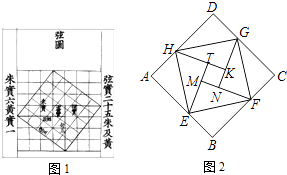
A.9
B.6
C.5
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚以400米/分的速度匀速骑车5分,在原地休息了6分,然后以500米/分的速度骑回出发地,下列函数图象能表达这一过程的是( )
A.
B.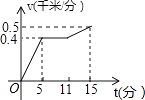
C.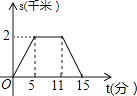
D.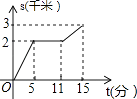
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com