
如图:一次函数的图象与反比例函数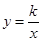 的图象交于A(-2,6)和点B(4,n)
的图象交于A(-2,6)和点B(4,n)
(1)求反比例函数的解析式和B点坐标
(2)根据图象回答,在什么范围时,一次函数的值大于反比例函数的值.
(1)反比例函数的解析式得: ,B的坐标是(4,﹣3);
,B的坐标是(4,﹣3);
(2)一次函数的值大于反比例函数的值时,x的范围是x<﹣2或0<x<4.
解析试题分析:(1)把A的坐标代入反比例函数的解析式即可求出反比例函数的解析式,把B的坐标代入即可求出B的坐标;
(2)根据A、B的坐标结合图象即可得出答案.
试题解析:(1)把A(﹣2,6)代入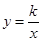 得:k=﹣12,
得:k=﹣12,
即反比例函数的解析式是: ,
,
把B(4,n)代入反比例函数的解析式得: ,
,
即B的坐标是(4,﹣3);
(2)∵一次函数和反比例函数的交点坐标是(4,﹣3)和(﹣2,6),
∴一次函数的值大于反比例函数的值时,x的范围是x<﹣2或0<x<4.
考点:反比例函数与一次函数的交点.


科目:初中数学 来源: 题型:解答题
如图,直线 ,
, 相交于点
相交于点 ,
, 与
与 轴的交点坐标为
轴的交点坐标为 ,
, 与
与 轴的交点坐标为
轴的交点坐标为 ,结合图象解答下列问题:(每小题4分,共8分)
,结合图象解答下列问题:(每小题4分,共8分)
(1)求直线 表示的一次函数的表达式;
表示的一次函数的表达式;
(2)当 为何值时,
为何值时, ,
, 表示的两个一次函数值都大于
表示的两个一次函数值都大于 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为了落实党中央提出的“惠民政策”,我市今年计划开发建设A、B两种户型的“廉租房”共40套.投入资金不超过200万元,又不低于198万元.开发建设办公室预算:一套A型“廉租房”的造价为5.2万元,一套B型“廉租房”的造价为4.8万元.
(1)请问有几种开发建设方案?
(2)哪种建设方案投入资金最少?最少资金是多少万元?
(3)在(2)的方案下,为了让更多的人享受到“惠民”政策,开发建设办公室决定通过缩小“廉租房”的面积来降低造价、节省资金.每套A户型“廉租房”的造价降低0.7万元,每套B户型“廉租房”的造价降低0.3万元,将节省下来的资金全部用于再次开发建设缩小面积后的“廉租房”,如果同时建设A、B两种户型,请你直接写出再次开发建设的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,已知点A(0,12),B(16,0),动点P从点A开始在线段AO上以每秒1个单位的速度向点O移动,同时点Q从点B开始在BA上以每秒2个单位的速度向点A移动,设点P、Q移动的时间为t秒。
⑴求直线AB的解析式;
⑵求t为何值时,△APQ与△AOB相似?
⑶当t为何值时,△APQ的面积为 个平方单位?
个平方单位?
⑷当t为何值时,△APQ的面积最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为保护学生视力,课桌椅的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为 cm,椅子的高度为
cm,椅子的高度为 cm,则
cm,则 应是
应是 的一次函数,下表列出两套符合条件的课桌椅的高度:
的一次函数,下表列出两套符合条件的课桌椅的高度:
| | 第一套 | 第二套 |
椅子高度 (cm) (cm) | 40 | 37 |
课桌高度 (cm) (cm) | 75 | 70 |
 与
与 的函数关系式.
的函数关系式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
一家图文广告公司制作的宣传画板颇受商家欢迎,这种画板的厚度忽略不计,形状均为正方形,边长在10~30dm之间.每张画板的成本价(单位:元)与它的面积(单位:dm2)成正比例,每张画板的出售价(单位:元)由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.在营销过程中得到了表格中的数据.
| 画板的边长(dm) | 10 | 20 |
| 出售价(元/张) | 160 | 220 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x2-6x+8=0的两个根(OA<OB),点C在y轴上,且OA︰AC=2︰5,直线CD垂直于直线AB于点P,交x轴于点D.
(1)求出点A、点B的坐标.
(2)请求出直线CD的解析式.
(3)若点M为坐标平面内任意一点,在坐标平面内是否存在这样的点M,使以点B、P、D、M为顶点的四边形是平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线y=- x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B'处.
x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B'处.
求: (1)点B'的坐标: .(2分)
(2)直线AM所对应的函数关系式.(8分)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知y+3与x+2成正比例,且当x=3时,y=7.
(1)写出y与x之间的函数关系式;
(2)当x=-1时,求y的值;
(3)当y=0时,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com