
如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是 .

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
随着人民生活水平的提高,购买老年代步车的人越来越多.这些老年代步车却成为交通安全的一大隐患.针对这种现象,某校数学兴趣小组在《老年代步车现象的调查报告》中就“你认为对老年代步车最有效的管理措施”随机对某社区部分居民进行了问卷调查,其中调查问卷设置以下选项(只选一项):
A:加强交通法规学习;
B:实行牌照管理;
C:加大交通违法处罚力度;
D:纳入机动车管理;
E:分时间分路段限行
调查数据的部分统计结果如下表:
| 管理措施 | 回答人数 | 百分比 |
| A | 25 | 5% |
| B | 100 | m |
| C | 75 | 15% |
| D | n | 35% |
| E |
| 25% |
| 合计 | a | 100% |
(1)根据上述统计表中的数据可得m= ,n= ,a= ;
(2)在答题卡中,补全条形统计图;
(3)该社区有居民2600人,根据上述调查结果,请你估计选择“D:纳入机动车管理”的居民约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
已知等腰三角形的两边长分別为a、b,且a、b满足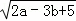 +(2a+3b﹣13)2=0,则此等腰三角形的周长为( )
+(2a+3b﹣13)2=0,则此等腰三角形的周长为( )
A. 7或8 B. 6或1O C. 6或7 D. 7或10
查看答案和解析>>
科目:初中数学 来源: 题型:
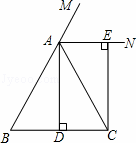
已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
为了大力宣传节约用电,某小区随机抽查了10户家庭的月用电量情况,统计如下表.关于这10户家庭的月用电量说法正确的是( )
月用电量(度) 25 30 40 50 60
户数 1 2 4 2 1
A. 中位数是40 B. 众数是4 C. 平均数是20.5 D. 极差是3
查看答案和解析>>
科目:初中数学 来源: 题型:
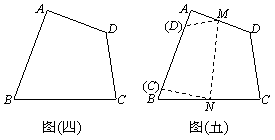
图(四)为某四边形ABCD纸片,其中ÐB=70°,ÐC=80°。若将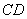 迭合在
迭合在 上,出现折线
上,出现折线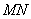 ,再将纸片展开后,M、N 两点分别在
,再将纸片展开后,M、N 两点分别在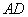 、
、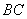 上,如图(五)所示,则ÐMNB的度数为何?
上,如图(五)所示,则ÐMNB的度数为何?
(A) 90 (B) 95 (C) 100 (D) 105
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知甲、乙两等差级数的项数均为6,甲、乙的公差相等,且甲级数的和与乙级数的和
相差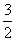 。若比较甲、乙的首项,较小的首项为1,则较大的首项为何?
。若比较甲、乙的首项,较小的首项为1,则较大的首项为何?
(A) 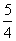 (B)
(B) 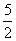 (C) 5 (D) 10
(C) 5 (D) 10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com