
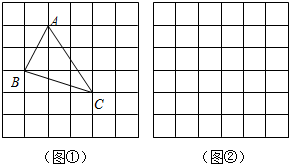
 (一)问题背景:小明是爱学习的人,通过网络搜索到有5种求三角形面积公式的方法.
(一)问题背景:小明是爱学习的人,通过网络搜索到有5种求三角形面积公式的方法.分析 (一)△ABC的面积=正方形的面积减去三个直角三角形的面积,即可得出结果;
(二)(1)先求出△ABC的面积,再由S=$\frac{1}{2}$ch,即可求出结果;
(2)由S=$\frac{abc}{4R}$,得出R=$\frac{abc}{4S}$,即可得出结果;
(三)仿照(一)和(二),容易得出题目.
解答 (一)解:知道,△ABC的面积是$\frac{7}{2}$;理由如下:
△ABC的面积=3×3-$\frac{1}{2}$×3×1-$\frac{1}{2}$×2×3-$\frac{1}{2}$×1×2=$\frac{7}{2}$;
故答案为$\frac{7}{2}$;
(二)解:(1)设AB边上的高为h,
则△ABC的面积S=$\frac{1}{2}$ch=4×4-$\frac{1}{2}$×4×1-$\frac{1}{2}$×1×3-$\frac{1}{2}$×3×4=$\frac{13}{2}$=$\frac{1}{2}$ch,
∴h=$\frac{13}{5}$,
即AB边上的高为$\frac{13}{5}$;
(2)∵S=$\frac{abc}{4R}$,
∴R=$\frac{abc}{4S}$=$\frac{5×\sqrt{17}×\sqrt{10}}{4×\frac{13}{2}}$=$\frac{{5\sqrt{170}}}{26}$;
即△ABC的外接圆半径为$\frac{{5\sqrt{170}}}{26}$.
(三)解:能,题目如下:
在△ABC中,AB=5,BC=$\sqrt{26}$,AC=$\sqrt{13}$,
求:(1)BC边上的高;
(2)△ABC的内切圆半径.
点评 本题是圆的综合题目,考查了三角形面积的几种计算方法、勾股定理等知识;本题有一定难度,综合性强,熟练掌握三角形面积的几种计算方法是解决问题的关键.


科目:初中数学 来源: 题型:填空题
 如图:直线y=kx(k>0)与双曲线$y=\frac{4}{x}$交于A(x1,y1)、B(x2,y2)两点,则2x1y2-3x2y1的值等于4.
如图:直线y=kx(k>0)与双曲线$y=\frac{4}{x}$交于A(x1,y1)、B(x2,y2)两点,则2x1y2-3x2y1的值等于4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1<y2 | C. | .y1≥y2 | D. | y1≤y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
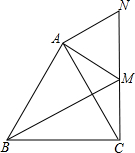 如图,△ABC和△AMN均为等边三角形,边长分别为$\sqrt{3}$,1.连接BM,CM,若BM⊥AC.
如图,△ABC和△AMN均为等边三角形,边长分别为$\sqrt{3}$,1.连接BM,CM,若BM⊥AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
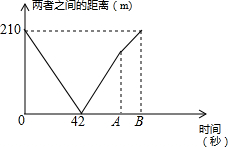 张宇和孙宁两人同时从自己家出发到对方家去,张宇以每秒3米的速度走向张宇家,孙宁也以一定的速度走向张宇家.如图是两人出发后,时间与两人之间距离关系的图象.
张宇和孙宁两人同时从自己家出发到对方家去,张宇以每秒3米的速度走向张宇家,孙宁也以一定的速度走向张宇家.如图是两人出发后,时间与两人之间距离关系的图象.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com