考点:二次函数图象上点的坐标特征
专题:规律型
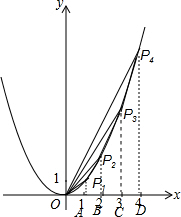
分析:作P1A⊥x轴于A,P2B⊥x轴于B,P3C⊥x轴于C,P4D⊥x轴于D,如图,根据二次函数图象上点的坐标特征可计算出P1点的坐标为(1,2),P2点的坐标为(2,8),P3点的坐标为(3,18),P4点的坐标为(4,32),再利用面积的和差分别计算出S1=S△OP1P2=S△OP2B-S△OP1A-S梯形P1ABP2=1×2,S2=S△OP2P3=S△OP3C-S△OP2B-S梯形P2BCP3=2×3,S3=S△OP3P4=S△OP4D-S△OP3C-S梯形P3CDP4=3×4,观察面积与三角形脚标的数字之间的关系易得S10=S△OP10P11=10×11=110.
解答:解
:作P
1A⊥x轴于A,P
2B⊥x轴于B,P
3C⊥x轴于C,P
4D⊥x轴于D,如图,
P
1点的坐标为(1,2),P
2点的坐标为(2,8),P
3点的坐标为(3,18),P
4点的坐标为(4,32),
S
1=S
△OP1P2=S
△OP2B-S
△OP1A-S
梯形P1ABP2=
×2×8-
×1×2-
×(2+8)×1=2=1×2,
S
2=S
△OP2P3=S
△OP3C-S
△OP2B-S
梯形P2BCP3=
×3×18-
×2×8-
×(8+18)×1=6=2×3,
S
3=S
△OP3P4=S
△OP4D-S
△OP3C-S
梯形P3CDP4=
×4×32-
×3×18-
×(18+32)×1=12=3×4,
所以S
10=S
△OP10P11=10×11=110.
故选D.
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了三角形的面积公式.

 如图,P1、P2、P3…Pk分别是抛物线y=2x2上的点,其横坐标分别是1,2,3…k,记△OP1P2的面积为S1,△OP2P3的面积为S2,△OP3P4的面积为S3,…则S10等于( )
如图,P1、P2、P3…Pk分别是抛物线y=2x2上的点,其横坐标分别是1,2,3…k,记△OP1P2的面积为S1,△OP2P3的面积为S2,△OP3P4的面积为S3,…则S10等于( ) :作P1A⊥x轴于A,P2B⊥x轴于B,P3C⊥x轴于C,P4D⊥x轴于D,如图,
:作P1A⊥x轴于A,P2B⊥x轴于B,P3C⊥x轴于C,P4D⊥x轴于D,如图,

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案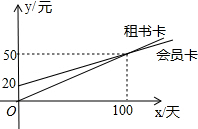 某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如图所示.
某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如图所示.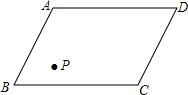 韩霜家为了扩大种植养殖规模,准备承包一片土地,镇政府把一片平行四边形土地ABCD分给韩霜和邻居张大伯家,每家一半.由于在这块田地里有一水井P(如图所示),两家为了都能方便地使用这口井,在划分时犯了难,你有解决的办法吗?
韩霜家为了扩大种植养殖规模,准备承包一片土地,镇政府把一片平行四边形土地ABCD分给韩霜和邻居张大伯家,每家一半.由于在这块田地里有一水井P(如图所示),两家为了都能方便地使用这口井,在划分时犯了难,你有解决的办法吗? 如图,△ABC在平面直角坐标系中,点M在AB上,点A,B,C,O,M均在网格的格点上.
如图,△ABC在平面直角坐标系中,点M在AB上,点A,B,C,O,M均在网格的格点上.