
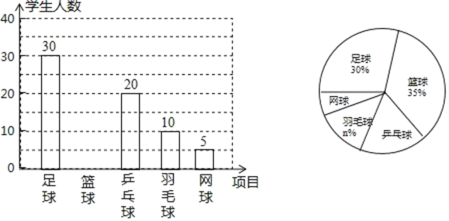
【题目】深圳高级中学(集团)开展“阳光体育活动”,共开设足球,蓝球,乒乓球,羽毛球,网球五项活动,为了了解学生对这五项活动的喜爱情况,随机调查了m名学生(每名学生必须且只能选择这五项运动中的一种),并根据调查的结果绘制了如图所示不完整的统计图.根据以上统计图提供的信息,解答下列问题:
(1)m= ,n= ;
(2)补全条形统计图;
(3)若深高(集团)共有学生6000人,则喜欢乒乓球的约有多少人?
【答案】(1)![]() ;(2)答案见解析;(3)1200.
;(2)答案见解析;(3)1200.
【解析】
(1)根据条形统计图中喜欢足球的人数以及扇形统计图中的喜欢足球人数所占的百分比即可求出总人数m的值,再根据条形统计图中喜欢羽毛球的人数即可求出喜欢羽毛球的人数所占的百分比,即可求出n的值;
(2)结合(1)中求得的总人数即可计算得到喜欢篮球人数,再补全条形统计图即可;
(3)可根据以样本估计总量,先求出抽样调查中喜欢乒乓球的人数占样本总数的比值,再根据总人数乘以比值估计总人数中喜欢乒乓球的人数即可.
(1)通过条形统计图可得到喜欢足球的人数为30人,通过扇形统计图中的喜欢足球人数所占的百分比为30%,即可求出总人数![]() 人;根据条形统计图中羽毛球的人数为10人,即可求出羽毛球所占的百分比
人;根据条形统计图中羽毛球的人数为10人,即可求出羽毛球所占的百分比![]() ,即n=10;
,即n=10;
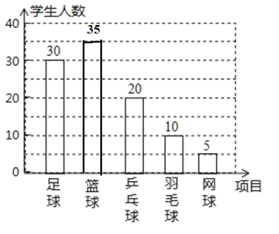
(2)喜欢篮球的人数=总人数-喜欢足球人数-喜欢乒乓球人数-喜欢羽毛球人数-喜欢网球人数=![]() 人,补全条形统计图如下图所示:
人,补全条形统计图如下图所示:
(3)已知在抽样调查的100人中喜欢乒乓球的人数所占的百分比![]() ,以样本估计总量得6000人中喜欢乒乓球的人数所占的百分比也约为20%,所以6000人中喜欢乒乓球的人数约为
,以样本估计总量得6000人中喜欢乒乓球的人数所占的百分比也约为20%,所以6000人中喜欢乒乓球的人数约为![]() 人.
人.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() ;
;
(5)![]() ;
;
(6)![]() ;
;
(7)![]() ;
;
(8)![]() ;
;
(9)![]() ;
;
(10)![]() ;
;
(11)20032;
(12)![]() ;
;
(13)![]() ;
;
(14)![]() ;
;
(15)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
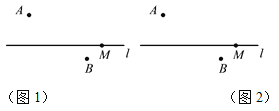
【题目】作图题:已知点A,点B,直线l及l上一点M.
(1)如图1,连接MA,并在直线l上作出一点N,使得点N在点M的左边,且满足MN=MA,作线段MN的中点C,连接BC;
(2)如图2,请在直线l上确定一点O,使点O到点A与点O到点B的距离之和最短,并写出画图的依据.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△CDE是以C为公共顶点的两个等腰三角形,且AC=CB,CD=CE,连接BD、AE相交于点M,连接CM,∠CAB=∠CDE=50°,则∠BMC=( )

A. 30°B. 40°C. 50°D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
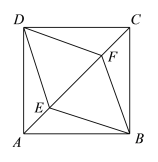
【题目】如图,E,F是正方形ABCD的对角线AC上的两点,且AE=CF.
(1)求证:四边形BEDF是菱形;
(2)若正方形ABCD的边长为4,AE=![]() ,求菱形BEDF的面积.
,求菱形BEDF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】窗户的形状如图所示(图中长度单位:cm),其上部是半圆形,下部是边长相同的四个小正方形,已知下部小正方形的边长是acm,计算:
(1)窗户的面积;
(2)窗户的外框的总长.
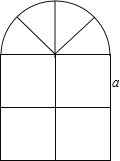
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com