
【题目】如图所示,在平行四边形ABCD中,⊙O是△ABC的外接圆,CD与⊙O相切于点C,点P是劣弧BC上的一个动点(点P不与点B、C重合),连结PA、PB、PC.
(1)求证:![]() ;
;
(2)当![]() 时,试判断△APC与△CBA是否全等,请说明理由;
时,试判断△APC与△CBA是否全等,请说明理由;
(3)填空:当![]() 的度数为_________时,四边形ABCD是菱形.
的度数为_________时,四边形ABCD是菱形.

【答案】(1)见解析;(2)全等,见解析;(3)60°
【解析】
(1)连接CO交AB于点E,由CD与圆O相切于点C,得到CE⊥CD,因为四边形ABCD为平行四边形,所以AB∥CD,因此CE⊥AB,所以AE=BE,于是CA=CB;
(2)当AC=AP时,△CPA≌△ABC.由于AC=BC,AC=AP,则∠ABC=∠BAC,∠APC=∠ACP,根据圆周角定理得∠ABC=∠APC,则∠BAC=∠ACP,加上AC=CA,即可得到△CPA≌△ABC;
(3)如图2,连接OC,AC,OB,根据平行线的性质得到∠BCD=120°,根据切线的性质得到∠OCD=90°,推出BO垂直平分AC,即可得到结论.
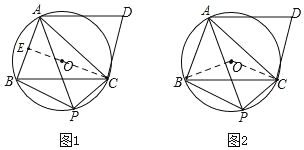
如图1,连接CO交AB于点E,
∵CD与圆O相切于点C,
∴CE⊥CD,
∵四边形ABCD为平行四边形,
∴AB∥CD,
∴CE⊥AB,
∴AE=BE,
∴CA=CB;
(2)当AP=AC时,△APC≌△CBA,理由如下:
∵CA=CB,AP=AC
∴∠ABC=∠BAC,∠APC=∠ACP,
∵∠ABC=∠APC,
∴∠BAC=∠ACP,
在△APC与△CBA中,
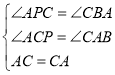
∴△APC≌△CBA(AAS);
(3)当∠ABC的度数为60°时,四边形ABCD是菱形,
如图2,连接OC,AC,OB,
∵∠ABC=60°,
∴∠BCD=120°,
∵CD与O相切于点C,
∴∠OCD=90°,
∴∠BCO=30°,
∵OB=OC,
∴∠OBC=30°,
∴∠ABO=30°,
∴BO垂直平分AC,
∴AB=BC,
∴四边形ABCD是菱形。
故答案为60°.


科目:初中数学 来源: 题型:
【题目】如图所示,线段AC是⊙O的直径,过A点作直线BF交⊙O于A、B两点,过A点作∠FAC的角平分线交⊙O于D,过D作AF的垂线交AF于E.
(1)证明DE是⊙O的切线;
(2)证明AD2=2AEOA;
(3)若⊙O的直径为10,DE+AE=4,求AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,以点A为圆心AB长为半径画弧交AD于点F,再分别以点B,F为圆心,大于![]() BF的长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.
BF的长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.
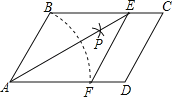
(1)求证:四边形ABEF是菱形;
(2)若∠C=60°,AE=4![]() ,求菱形ABEF的面积.
,求菱形ABEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为抛物线顶点;
为抛物线顶点;
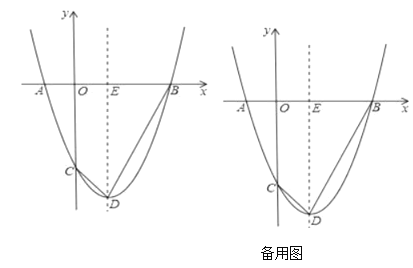
(1)求点![]() 和点
和点![]() 的坐标;
的坐标;
(2)连结![]() 、
、![]() ,抛物线的对称轴与
,抛物线的对称轴与![]() 轴交于点
轴交于点![]() .
.
①若线段![]() 上有一点
上有一点![]() ,使
,使![]() ,求点
,求点![]() 的坐标;
的坐标;
②若抛物线上一点![]() ,作
,作![]() ,交直线
,交直线![]() 于点
于点![]() ,使
,使![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
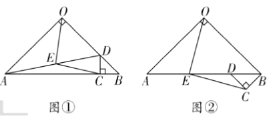
【题目】如图①,在![]() 中,
中,![]() 为
为![]() 边上一点,过
边上一点,过![]() 点作
点作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(观察猜想)
(1)①![]() 的数量关系是___________
的数量关系是___________
②![]() 的数量关系是______________
的数量关系是______________
(类比探究)
(2)将图①中![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(拓展迁移)
(3)将![]() 绕点
绕点![]() 旋转任意角度,若
旋转任意角度,若![]() ,请直接写出点
,请直接写出点![]() 在同一直线上时
在同一直线上时![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
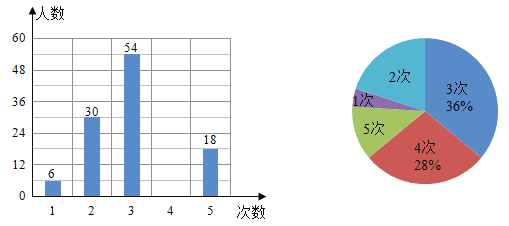
【题目】某市教育局组织全市中小学教师开展“访千家”活动.活动过程中,教育局随机抽取了近两周家访的教师人数及家访次数,将采集到的全部数据按家访次数分成五类,由甲、乙两人分别绘制了下面的两幅统计图(图都不完整).请根据以上信息,解答下列问题:
(1)请把这福条形统计图补充完整(画图后请标注相应的数据).
(2)在采集到的数据中,近两周平均每位教师家访___________次.
(3)若该市有12000名教师,求近两周家访不少于3次的教师约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明经过市场调查,整理出他妈妈商店里一种商品在第![]() 天的销售量的相关信息如下表:
天的销售量的相关信息如下表:
时间第 |
|
|
售价(元/件) |
| 50 |
每天销量(件) |
| |
已知该商品的进价为每件20元,设销售该商品的每天利润为![]() 元.
元.
(1)求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于2400元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了对该区八年级数学学科教学质量进行检查,对该区八年级的学生进行摸底,为了解摸底的情况,进行了抽样调查,过程如下,请将有关问题补充完整.
收集数据:随机抽取![]() 学校与
学校与![]() 学校的各20名学生的数学成绩(单位:分)进行
学校的各20名学生的数学成绩(单位:分)进行
| 91 | 89 | 77 | 86 | 71 | 31 | 97 | 93 | 72 | 91 |
81 | 92 | 85 | 85 | 95 | 88 | 88 | 90 | 44 | 91 | |
| 84 | 93 | 66 | 69 | 76 | 87 | 77 | 82 | 85 | 88 |
90 | 88 | 67 | 88 | 91 | 96 | 68 | 97 | 59 | 88 |
整理、描述数据:按如下数据段整理、描述这两组数据
分段 学校 | 30≤x≤39 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
| 1 | 1 | 0 | 0 | 3 | 7 | 8 |
|
分析数据:两组数据的平均数、中位数、众数、方差如下表:
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
| 81.85 | 88 | 91 | 268.43 |
| 81.95 | 86 | m | 115.25 |
得出结论:
![]() :若
:若![]() 学校有800名八年级学生,估计这次考试成绩80分以上(包含80分)人数为多少人?
学校有800名八年级学生,估计这次考试成绩80分以上(包含80分)人数为多少人?
![]() :根据表格中的数据,推断出哪所学校学生的数学水平较高,并说明理由.(至少从两个不同的角度说明推断的合理性)
:根据表格中的数据,推断出哪所学校学生的数学水平较高,并说明理由.(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣1,﹣1),点B(1,1),若抛物线y=x2﹣ax+a+1与线段AB有两个不同的交点(包含线段AB端点),则实数a的取值范围是( )
A.![]() ≤a<﹣1B.
≤a<﹣1B.![]() ≤a≤﹣1C.
≤a≤﹣1C.![]() <a<﹣1D.
<a<﹣1D.![]() <a≤﹣1
<a≤﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com