
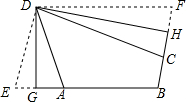
 定义:有三个内角相等的四边形叫三等角四边形.
定义:有三个内角相等的四边形叫三等角四边形.分析 (1)根据四边形的内角和是360°,确定出∠A的范围;
(2)由四边形DEBF为平行四边形,得到∠E=∠F,且∠E+∠EBF=180°,再根据等角的补角相等,判断出∠DAB=∠DCB=∠ABC,即可.
解答 解:(1)∵∠A=∠B=∠C,
∴3∠A+∠ADC=360°,
∴∠ADC=360°-3∠A.
∵0<∠ADC<180°,
∴0°<360°-3∠A<180°,
∴60°<∠A<120°;
(2)证明:∵四边形DEBF为平行四边形,
∴∠E=∠F,且∠E+∠EBF=180°.
∵DE=DA,DF=DC,
∴∠E=∠DAE=∠F=∠DCF,
∵∠DAE+∠DAB=180°,∠DCF+∠DCB=180°,∠E+∠EBF=180°,
∴∠DAB=∠DCB=∠ABC,
∴四边形ABCD是三等角四边形.
点评 本题主要考查了翻折变换-折叠问题,四边形的内角和是360°,平行四边形的性质,正方形的性质,勾股定理,解本题的关键是熟练掌握折叠的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
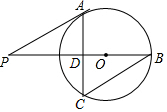 如图,已知⊙O的半径为5,PA是⊙O的一条切线,切点为A,连接PO并延长,交⊙O于点B,过点A作AC⊥PB交⊙O于点C、交PB于点D,连接BC,当∠P=30°时,
如图,已知⊙O的半径为5,PA是⊙O的一条切线,切点为A,连接PO并延长,交⊙O于点B,过点A作AC⊥PB交⊙O于点C、交PB于点D,连接BC,当∠P=30°时,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
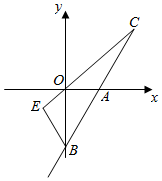 如图,直线y=2x-4与x轴交于点A,与y轴交于点B,与直线y=$\frac{1}{2}$x交于点C,E为射线CO上一点,且y轴平分∠EBC,求点E的坐标.
如图,直线y=2x-4与x轴交于点A,与y轴交于点B,与直线y=$\frac{1}{2}$x交于点C,E为射线CO上一点,且y轴平分∠EBC,求点E的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
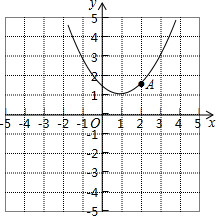 如图,抛物线y=$\frac{1}{2}$x2-x+c和反比例函数y=$\frac{k}{x}$的图象都经过A(2,1.5).
如图,抛物线y=$\frac{1}{2}$x2-x+c和反比例函数y=$\frac{k}{x}$的图象都经过A(2,1.5).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 15500(1+x)2=13000 | B. | 15500(1-x)2=13000 | C. | 13000(1+x)2=15500 | D. | 13000(1-x)2=15500 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
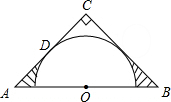 如图,在△ABC中,∠C=90°,AC=BC,AB=2,点O为AB的中点,以点O为圆心作半圆与边AC相切于点D.则图中阴影部分的面积为( )
如图,在△ABC中,∠C=90°,AC=BC,AB=2,点O为AB的中点,以点O为圆心作半圆与边AC相切于点D.则图中阴影部分的面积为( )| A. | 1-$\frac{1}{4}$π | B. | $\frac{1}{2}$-$\frac{π}{8}$ | C. | 2-$\frac{3π}{4}$ | D. | 2-$\frac{1}{4}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
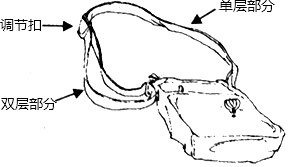 如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:| 单层部分的长度x(cm) | … | 4 | 6 | 8 | 10 | … | 150 |
| 双层部分的长度y(cm) | … | 73 | 72 | 71 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com